Soal 1
Sebuah batang bermassa 2M dan panjang L
dihubungkan ke dinding oleh sebuah engsel, dimana batang bebas berotasi.
Seutas tali mendatar yang dihubungkan ke ujung batang menahan batang
pada sudut θ terhadap arah vertikal, seperti ditunjukkan pada gambar.
Jika tiba-tiba tali putus, tentukan percepatan sudut batang!
Torsi pada titik O diakibatkan oleh gaya berat batang w karena ketika tali putus tegangan tali sama dengan nol (T = 0) dan gaya kontak engsel dan batang yaitu V dan H tidak menyebabkan momen gaya pada O.
Gaya w, lengan momen à OR = ½ L sin θ
Maka, resultan momen gaya pada titik O adalah
ΣτO = Iα à momen inersia batang pada salah satu ujungnya adalah I = 1/3 ML2
w x OR = (1/3 ML2)α
(w x ½ L sin θ) = (1/3 ML2)α
(Mg x ½ L sin θ) = (1/3 ML2)α
Soal 2
Silinder pejal dan bola pejal yang memiliki massa dan jari-jari yang sama dilepaskan dari keadaan diam dari sebuah bidang miring kasar dengan sudut kemiringan θ. Perbandingan percepatan yang dialami silinder dan bola tersebut adalah . . . .
A. 5 : 1
B. 2 : 1
C. 5 : 4
D. 1 : 2
E. 4 : 5
Jawab: C
∑F = ma
Mg sin θ – f = Ma (*)
Benda berotasi akibat gaya gesekan, maka
∑τ = Iα
fR = kMR2(a/R) karena a = αR
f = kMa (**)
dari (*) dan (**) kita peroleh
Mg sin θ – kMa = Ma
Sehingga,
a = g sin θ/(k + 1)
untuk silinder dan bola yang memiliki momen inersia masing-masing Isilinder = ½ MR2 dan Ibola = 2MR2/5, maka
as/ab = 5/4
Soal 3
Dua benda bermassa m1 = 5 kg dan m2 = 4 kg dihubungkan dengan seutas tali ringan melalui sebuah katrol dengan massa M = 2 kg dan jari-jari R = 10 cm. Massa m2 berada pada bidang miring licin dengan sudut kemiringan θ = 300. Tentukan: (a) percepatan sistem, (b) percepatan sudut katrol, dan (c) tegangan tali.
Jawab:
Gambar di bawah menunjukkan gaya-gaya yang bekerja pada benda dan katrol.
Hukum II Newton berlaku untuk kedua benda,
Benda m1:
50 N – T1 = 5a
T1 = 50 – 5a (*)
Benda m2:
T2 – 20 N = 4a
T2 = 20 + 4a (**)
Katrol:
∑τ = Iα
(T1 – T2)R = ½MR2(a/R)
T1 – T2 = ½Ma = a (***)
Dari persamaan (*), (**) dan (***) kita peroleh
50 – 5a – (20 + 4a) = a
a = 3 m/s2
maka percepatan sudut katrol adalah
α = a/R = 3 m/s2/0,1 m = 30 rad/s2
Tegangan pada kedua tali adalah
T1 = 50 – 5a = 35 N
T2 = 20 + 4a = 32 N
Soal 4
Sebuah bola pejal bermassa m = 5,0 kg berada diatas permukaan bidang miring yang kasar dengan sudut θ = 300 yang ditarik gaya F = 23 N seperti diperlihatkan gambar berikut!
B. 3,0 m/s2
C. 4,0 m/s2
D. 5,5 m/s2
E. 7,0 m/s2
Jawab:
Gaya-gaya yang bekerja pada bola diperlihatkan pada gambar di bawah ini!
F + f + (–mg sin θ) = ma (*)
Bola berotasi terhadap porosnya akibat adanya gaya gesek dan gaya F, maka
∑τ = Iα dengan a = αR, maka
–FR + fR = (–2mR2/5)(a/R)
F – f = 2ma/5
f = F – 2ma/5 (**)
Dari (*) dan (**) kita peroleh
F + (F – 2ma/5) + (–mg sin θ) = ma
2F – mg sin θ = 7ma/5
a = 5[2F – mg sin θ]/7m
a = 5[2 x 23 N – 50(1/2)]/(7 x 5 kg) = 3,0 m/s2
Solusi:
Tentunya batang berotasi pada engselnya (poros O), maka gaya-gaya yang bekerja pada batang ditunjukkan pada gambar di bawah ini,Torsi pada titik O diakibatkan oleh gaya berat batang w karena ketika tali putus tegangan tali sama dengan nol (T = 0) dan gaya kontak engsel dan batang yaitu V dan H tidak menyebabkan momen gaya pada O.
Gaya w, lengan momen à OR = ½ L sin θ
Maka, resultan momen gaya pada titik O adalah
ΣτO = Iα à momen inersia batang pada salah satu ujungnya adalah I = 1/3 ML2
w x OR = (1/3 ML2)α
(w x ½ L sin θ) = (1/3 ML2)α
(Mg x ½ L sin θ) = (1/3 ML2)α
Soal 2
Silinder pejal dan bola pejal yang memiliki massa dan jari-jari yang sama dilepaskan dari keadaan diam dari sebuah bidang miring kasar dengan sudut kemiringan θ. Perbandingan percepatan yang dialami silinder dan bola tersebut adalah . . . .
A. 5 : 1
B. 2 : 1
C. 5 : 4
D. 1 : 2
E. 4 : 5
Jawab: C
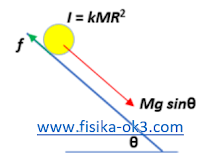
Gambar di atas menunjukkan sebuah benda yang dengan momen inersia I = kMR2 berotasi menuruni bidang miring, menurut hukum II Newton kita peroleh
∑F = ma
Mg sin θ – f = Ma (*)
Benda berotasi akibat gaya gesekan, maka
∑τ = Iα
fR = kMR2(a/R) karena a = αR
f = kMa (**)
dari (*) dan (**) kita peroleh
Mg sin θ – kMa = Ma
Sehingga,
a = g sin θ/(k + 1)
untuk silinder dan bola yang memiliki momen inersia masing-masing Isilinder = ½ MR2 dan Ibola = 2MR2/5, maka
as/ab = 5/4
Soal 3
Dua benda bermassa m1 = 5 kg dan m2 = 4 kg dihubungkan dengan seutas tali ringan melalui sebuah katrol dengan massa M = 2 kg dan jari-jari R = 10 cm. Massa m2 berada pada bidang miring licin dengan sudut kemiringan θ = 300. Tentukan: (a) percepatan sistem, (b) percepatan sudut katrol, dan (c) tegangan tali.
Jawab:
Gambar di bawah menunjukkan gaya-gaya yang bekerja pada benda dan katrol.
Benda m1:
50 N – T1 = 5a
T1 = 50 – 5a (*)
Benda m2:
T2 – 20 N = 4a
T2 = 20 + 4a (**)
Katrol:
∑τ = Iα
(T1 – T2)R = ½MR2(a/R)
T1 – T2 = ½Ma = a (***)
Dari persamaan (*), (**) dan (***) kita peroleh
50 – 5a – (20 + 4a) = a
a = 3 m/s2
maka percepatan sudut katrol adalah
α = a/R = 3 m/s2/0,1 m = 30 rad/s2
Tegangan pada kedua tali adalah
T1 = 50 – 5a = 35 N
T2 = 20 + 4a = 32 N
Soal 4
Sebuah bola pejal bermassa m = 5,0 kg berada diatas permukaan bidang miring yang kasar dengan sudut θ = 300 yang ditarik gaya F = 23 N seperti diperlihatkan gambar berikut!
Percepatan gerak bola jika jari-jarinya adalah R = 10 cm adalah . . . .
A. 1,5 m/s2B. 3,0 m/s2
C. 4,0 m/s2
D. 5,5 m/s2
E. 7,0 m/s2
Jawab:
Gaya-gaya yang bekerja pada bola diperlihatkan pada gambar di bawah ini!
Berlaku hukum II Newton pada bola, sehingga
F + f + (–mg sin θ) = ma (*)
Bola berotasi terhadap porosnya akibat adanya gaya gesek dan gaya F, maka
∑τ = Iα dengan a = αR, maka
–FR + fR = (–2mR2/5)(a/R)
F – f = 2ma/5
f = F – 2ma/5 (**)
Dari (*) dan (**) kita peroleh
F + (F – 2ma/5) + (–mg sin θ) = ma
2F – mg sin θ = 7ma/5
a = 5[2F – mg sin θ]/7m
a = 5[2 x 23 N – 50(1/2)]/(7 x 5 kg) = 3,0 m/s2





thank youu
ReplyDeleteTerimakasih
ReplyDelete