Energi merupakan salah satu konsep terpenting dalam sains. Namun
tidak terdapat sebuah definisi umum yang sederhana untuk energi.Walau
begitu, untuk tiap-tiap jenis energi yang spesifik, kita dapat membuat
definisi yang cukup sederhana. Di bagian ini kita akan mendefinisikan
energi kinetik (gerak) translasi dan beberapa jenis energi potensial.
Kita dapat mendefinisikan energi sebagai kemampuan melakukan usaha.
Definisi sederhana ini dapat tidak akurat, dan tidak pula selalu valid
untuk semua tipe energi. Tetapi definisi ini selalu valid untuk energi
mekanik yang akan kita bahas dalam bagian berikutnya, dan dapat
digunakan untuk menjelaskan secara gamblang tentang hubungan antara
usaha dan energi. Kita terlebih dahulu mendefinisikan energi kinetik
suatu benda.
Sebuah benda yang bergerak dapat melakukan usaha pada benda lain yang ditumbuknya. Sebuah peluru meriam yang sedang melesat melakukan usaha pada dinding batu yang dihantamnya; sebuah martil yang sedang mengayun melakukan usaha pada paku yang ditumbuknya masuk ke dalam kayu.
 |
| Gambar (1) |
 |
| Gambar (2) |
Dalam masing-masing kasus ini, sebuah benda yang sedang bergerak
memberikan gaya pada benda lainnya yang kemudian mengalami perpindahan
akibat kerja gaya itu. Sebuah benda yang sedang bergerak memiliki
kemampuan untuk melakukan usaha dan karenanya dapat dikatakan memiliki
energi. Energi pada benda-benda yang bergerak, atau energi gerak disebut
energi kinetik (kinetic energy).
Gambar (2) merupakan sebuah balok bermassa m yang sedang bergerak dalam sebuah lintasan lurus dengan kecepatan awal v1. Untuk mempercepat gerakan benda hingga mencapai kecepatan v2, gaya total konstan ΣF diberikan pada benda itu ke arah yang sejajar dengan arah gerakannya selama terjadinya perpindahan sejauh ∆x. Maka usaha total yang dilakukan pada benda tersebut adalah Wtotal = ΣF.∆x. Dengan menggunakan hukum kedua newton ΣF = m.a, dan dengan persamaan pada gerak pada percepatan konstan yaitu a = (v22 – v12)/2.∆x. Di mana v1 sebagai kecepatan awal dan v2 adalah kecepatan akhir benda. kemudian, mensubtitusikan bentuk ini ke dalam ΣF = ma, kita menentukan usaha yang di lakukan
Kita mendefinisikan bagian ½ mv2 sebagai energi kinetik kinetik translasi dari benda yang kita bicarakan.
Ek = ½mv2 (2)
Persamaan (2) merupakan energi kinetik suatu benda pada gerak satu
dimensi dan untuk gaya konstan, berlaku secara umum bagi gerak translasi
benda-benda dalam tiga dimensi dan juga untuk kasus-kasus yang
melibatkan gaya yang berubah-ubah.
Kita dapat menulis kembali persamaan (1) menjadi
Wtotal = Ek2 – Ek1
Atau Wtotal = ∆Ek = ½ mv22 – ½ mv12 (3)
Persamaan (3) atau (1) merupakan sebuah rumusan penting yang dikenal sebagai prinsip usaha-energi (work-energy principle). Prinsip ini dapat dinyatakan sebagai
Usaha total yang dilakukan pada sebuah benda adalah sama dengan perubahan energi kinetik pada benda tersebut.
CATATAN: (perhatikan bahwa di sini kita menggunakan hukum kedua Newton, Ftotal = ma, di mana Ftotal
ini merupakan resultan gaya yang tidak lain merupakan total gaya yang
bekerja pada benda yang bersangkutan. Sehingga prinsip usaha energi
hanya berlaku bila W adalah usaha total yang dilakukan pada benda. Jelasnya usaha yang dihasilkan oleh semua gaya yang bekerja pada benda tersebut.)
Prinsip usaha-energi merupakan perumusan ulang yang sangat berguna
dari hukum-hukum gerak newton. Prinsip ini memberitahukan kita bahwa
jika usaha total (positif) W yang dilakukan pada benda, maka energi energi kinetik benda itu akan berkurang sebesar W.
Jelasnya, gaya total yang diberikan pada sebuah benda melawan arah
gerakan benda dan akan mengurangi kecepatan benda itu dan juga energi
kinetiknya. Salah satu contohnya adalah sebuah palu (martil) yang sedang bergerak mengayun, gambar (3) dan menghantam sebuah paku. Gaya total pada martil itu (-F, dalam gambar (3), di mana F diasumsikan konstan untuk penyederhanaan) bekerja ke arah kiri, sedangkan perpindahan martil itu ∆x mengarah ke kanan.
Maka, usaha total yang dilakukan pada martil, W = (F)(∆x)(cos 1800) = – F ∆x, bernilai negatif dan karenanya energi kinetik martil berkurang dan (biasanya menjadi nol).
Gambar (3) yang mengilustrasikan bagaimana energi dapat dipandang
sebagai kemampuan melakukan usaha. Ketika bergerak melambat, martil
melakukan usaha positif pada paku: W = (+F)(+ ∆x) yang nilainya positif. Pengurangan energi kinetik martil (= F∆x berdasarkan persamaan (3)) adalah sama dengan usaha yang dapat dilakukan martil pada benda lainnya, dalam kasus ini pada paku.
 |
| Gambar (3) |
Energi kinetik translasi (=1/2 mv2) berbanding
lurus dengan massa benda yang bersangkutan, energi ini juga sebanding
dengan kuadrat kecepatan benda itu. Sehingga, jika massa benda
dilipat-duakan, maka energi kinetiknya juga akan berlipat dua. Tetapi,
jika kecepatan benda dilipat-duaknya, maka energi kinetik benda empat
kali lebih besar dari semula dan karenanya memiliki kemampuan melakukan
usaha empat kali lebih banyak.
Karena terdapat hubungan langsung antara usaha dan energi kinetik
ini, persamaan (3), energi diukur dengan satuan yang sama seperti halnya
usaha: joule dalam sistem SI, erg dalam sistem cgs, dan kaki-pound
dalam sistem Inggris. Sebagaimana halnya usaha, energi kinetik adalah
sebuah besaran skalar. Energi kinetik dari sekelompok benda adalah
jumlah (aljabar) dari energi kinetik yang dimiliki oleh masing-masing
benda di dalam kelompok tersebut.
Prinsip usaha-energi dapat diterapkan kepada partikel dan juga kepada objek yang dapat diaprosimasikan sebagai partikel.
Contoh Soal 1
Berapa besar usaha total yang diperlukan untuk menaikan kecepatan sebuah mobil bermassa 1000 kg dari 20 m/s menjadi 30 m/s.
Jawab:
Sebuah mobil adalah sistem yang kompleks. Mesin mobil memutar
roda-roda yang mendorong permukaan jalan, dan permukaan jalan memberikan
reaksinya kembali, gambar (4). Kita tidak perlu memperhatikan kerumitan
itu saat itu. Kita mungkin mendapatkan hasil yang berguna melalui
prinsip usaha-energi, tetapi hanya jika kita memodelkan (menganggap)
mobil tersebut sebagai partikel.diperlukan adalah sama dengan
pertambahan energi kinetik mobil tersebut.
Usaha total yang diperlukan adalah sama dengan pertambahan energi kinetik mobil tersebut:
Wtotal = ∆Ek = ½ mv22 – ½ mv12
= ½ (1000 kg)(30 m/s)2 – ½ (1000 kg)(20 m/s)2
= 250 kJ
= 250 kJ
Contoh Soal 2
Berapa usaha yang harus dilakukan untuk menghentikan sebuah mobil bermassa 925 kg yang sedang melaju dengan kecepatan 90 km/jam?
Jawab:
Menghentikan mobil dari v1 = 90 km/jam = 20 m/s sampai berhenti (v2 = 0), maka
Wtotal = ∆Ek = ½ mv22 – ½ mv12
= ½ (925 kg)(0)2 – ½ (925 kg)(20 m/s)2
= –185 kJ
Tanda negatif menunjukkan bahwa energi kinetik mobil berkurang!
Contoh soal 3
Berapa besar gaya yang dibutuhkan untuk mempercepat sebuah mobil 1300
kg dari keadaan diam hingga mencapai kecepatan 20 m/s setelah mencapai
jarak tempuh 80 m?
Jawab:
W = ∆Kà ∆K = ½ mv2 – 0 = ½ (1300 kg)(20 m/s)2 = 260 kJ.
Sedangkan W = F.∆x = F (80 m).
Sehingga didapat: 80F = 260 kJ,
F = 260/60 N = 3,25 N
Contoh Soal 4
 Sebuah balok seberat 6,0 kg yang awalnya berada dalam posisi diam
ditarik ke kanan di sepanjang sebuah permukaan bidang horisontal yang
licin oleh sebuah gaya horisontal konstan sebesar F = 12 N. (a)
Carilah kelajuan balok setelah dipindahkan sejauh 3,0 m. Bagaimana
jika? Kita misalkan besar gaya digandakan menjadi F’ = 2F. Balok seberat 6,0 kg mengalami percepatan 3,5 m/s karena gaya ini, sementara balok bergerak sepanjang perpindahan ∆x’. (b) bagaimana perpindahan ∆x’ dibandingkan dengan perpindahan awal ∆x? (c) bagaimana selang waktu ∆t’ yang dibutuhkan balok untuk mempercepat geraknya dari keadaan diam sampai mencapai 3,5 m/s dibandingkan dengan ∆t?
Sebuah balok seberat 6,0 kg yang awalnya berada dalam posisi diam
ditarik ke kanan di sepanjang sebuah permukaan bidang horisontal yang
licin oleh sebuah gaya horisontal konstan sebesar F = 12 N. (a)
Carilah kelajuan balok setelah dipindahkan sejauh 3,0 m. Bagaimana
jika? Kita misalkan besar gaya digandakan menjadi F’ = 2F. Balok seberat 6,0 kg mengalami percepatan 3,5 m/s karena gaya ini, sementara balok bergerak sepanjang perpindahan ∆x’. (b) bagaimana perpindahan ∆x’ dibandingkan dengan perpindahan awal ∆x? (c) bagaimana selang waktu ∆t’ yang dibutuhkan balok untuk mempercepat geraknya dari keadaan diam sampai mencapai 3,5 m/s dibandingkan dengan ∆t?
Jawab:
(a) Gaya total yang bekerja pada balok adalah F = 12 N, usaha yang dilakukan oleh gaya ini adalah
W = F.∆x = (12 N)(3,0 m) = 36 J
Dengan menggunakan teorema usaha-energi kinetik dan mengamati bahwa energi kinetik awalnya adalah nol (bergerak dari keadaan diam), kita mendapatkan
W = Ek2 – Ek1 = ½ mv22 – 0
(b) Jika kita menarik lebih keras, maka kelajuan baloknya akan lebih tinggi dalam jarak yang lebih pendek sehingga kita perkirakan ∆x’ < ∆x. Secara matematis, dari teorema usaha-energi kinetik W = ∆Ek, kita peroleh
F’∆x’ = ∆Ek = F.∆x
∆x’ = (F/F’)∆x = ½ ∆x.
dan jaraknya adalah lebih pendek, sama seperti argumen kita.
(c) Jika kita menarik lebih keras, maka kelajuan baloknya akan lebih tinggi dalam selang waktu lebih pendek sehingga kita perkirakan ∆t’ < ∆t. Secara matematis, dari definisi tentang kelajuan rata-rata
Oleh karena, baik gaya awal maupun gaya yang digandakan mengakibatkan
perubahan yang sama dalam kelajuan, kelajuan rata-rata adalah sama pada
kedua kasus. Maka,
dan selang waktunya adalah lebih pendek, sesuai dengan argumen kita.
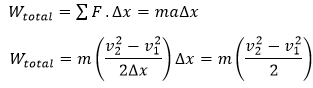



Post a Comment for "Energi Kinetik dan Prinsip Usaha- Energi"
Sobat Fisika! Berikan Komentar di kolom komentar dengan bahasa yang sopan dan sesuai isi konten...Terimasih untuk kunjunganmu di blog ini, semoga bermanfaat!