Persamaan Umum Gelombang Mekanik (Deskripsi Matematis)

Banyak karakteristik gelombang periodik yang dapat dijelaskan dengan menggunakan konsep laju gelombang, periode gelombang, dan panjang gelombang. Akan tetapi, seringkali kita memerlukan deskripsi yang lebih rinci mengenai posisi dan gerak partikel yang bergetar. Untuk maksud ini kita dapat menggunakan konsep fungsi gelombang, yaitu suatu fungsi yang menjelaskan posisi partikel yang bergetar pada sembarang waktu.

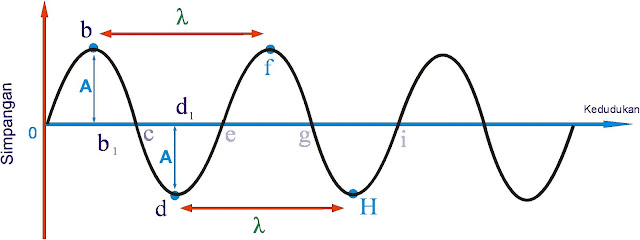Gambar 1, bentuk gelombang transversal pada tali

Kita akan meninjau gelombang pada dawai yang diregangkan. Pada posisi setimbang, dawai membentuk garis lurus. Kita menganggap bahwa garis lurus ini merupakan sumbu-x dalam sistem koordinat kartesius. Getaran dawai membentuk gelombang transversal sehingga selama geraknya seluruh partikel dengan posisi setimbang sepanjang sumbu-x digeser sejauh y yang arahnya tegak lurus sumbu-x ini. Nilai y bergantung pada posisi partikel yang ditinjau dan juga bergantung pada waktu. Secara matematis, y merupakan fungsi dari x dan t atau sering ditulis y = y(x,t) Ungkapan y(x,t) disebut sebagai fungsi gelombang. Jika fungsi gelombang diketahui, kita dapat menentukan pergeseran partikel yang bergetar (diukur dari posisi setimbang) pada sembarang waktu.

Sekarang kita akan membicarakan bentuk fungsi gelombang untuk gelombang sinusoidal, yaitu gelombang sinusoidal yang berjalan dari kiri ke kanan sepanjang dawai. Diandaikan pergeseran partikel di ujung kiri dawai (x = 0) dinyatakan dengan persamaan

Artinya, partikel itu bergerak harmonik sederhana dengan amplitudo A, frekuensi f, dan frukuensi sudut ω = 2πft. Pada t = 0 partikel di x = 0 memiliki pergeseran nol (y = 0) dan partikel sedang bergerak ke arah sumbu-y positif. Gelombang ini merambat dari x = 0 ke titik x di sebelah kanan titik asal dalam waktu x/v dengan v laju gelombang. Jadi, gerakan di titik x pada waktu t sama seperti gerakan di titik x = 0 pada waktu sebelumnya, yaitu t – (x/v). Dengan demikian, kita dapat menghitung pergeseran di titik x pada waktu t hanya dengan mengganti t pada Persamaan (1) dengan t – (x/v).  Jadi,

Kita dapat menuliskan fungsi gelombang Persamaan (2) menjadi beberapa bentuk yang berbeda. Dengan mengingat f = 1/T dan λ = v/f = vT Persamaan (2) menjadi

Bilangan gelombang, dengan simbol k, didefinisikan sebagai 

Dengan substitusi λ = 2π/k dan f = ω/2π ke Persamaan (1), diperoleh

Dengan demikian, Persamaan (2) menjadi

Kita dapat memodifikasi Persamaan (2) sampai dengan Persamaan (6) untuk menjelaskan gelombang yang merambat ke arah sumbu-x negatif. Dalam kasus ini, pergeseran di titik x pada saat t adalah sama seperti gerak di titik x = 0 pada waktu sesudahnya, yaitu t + (x/v). Dengan demikian, kita dapat mengganti t pada Persamaan (1) dengan t + (x/v). Jadi, untuk gelombang yang merambat ke arah sumbu-x negatif berlaku

Secara umum, fungsi gelombang dapat dituliskan sebagai

 Tanda positif menunjukkan gelombang merambat ke arah sumbu-x negatif, sedangkan tanda negatif menunjukkan gelombang merambat ke arah sumbu-x positif. Besaran (ωt ± kx) dinamakan sudut fase, dengan satuan derajat atau radian. Titik-titik yang pergeserannya maksimum, yaitu y = A terjadi ketika sin (ωt ± kx) = 1. Sudut fase pada saat pergeseran maksimum adalah π/2, 5π/2 dan seterusnya. Titik-titik yang pergeserannya minimum, yaitu y = 0 terjadi ketika  sudut fasenya adalah 0, π, 2π dan seterusnya. Dua titik A dan B dikatakan memiliki fase sama apabila kedua titik ini memiliki beda sudut fase sebesar 2π  atau 2nπ, dengan n bilangan bulat. Apabila dua titik memiliki fase yang sama, maka kedua titik tersebut bergerak dalam arah yang sama.

Share :