Gejala gelombang secara umum dapat didefenisikan sebagai rambatan
gangguan periodik melalui zat perantara. Perambatan gelombang ini
berlangsung, bergantung pada gaya-gaya yang bekerja antarpartikel zat
perantaranya.
Oleh karena itu, tidak mengherankan mengapa setelah segera setelah Maxwell memperlihatkan bahwa kehadiran gelombang elektromagnet diramalkan berdasarkan persamaan-persamaan elektromagnet klasik, para fisikawan segera melakukan berbagai upaya untuk mempelajari sifat zat perantara yang berperan bagi perambatan gelombang elektromagnet ini. Zat perantara ini disebut eter, namun karena zat ini belum pernah teramati dalam percobaan, maka dipostulatkan bahwa ia tidak bermassa dan tidak tampak, tetapi mengisi seluruh ruang, dan fungsi satu-satunya untuk merambatkan gelombang elektromagnet.
Konsep eter ini sangat menarik karena; pertama, sulit untuk membayangkan bagaimana sebuah gelombang dapat merambat tanpa memerlukan zat perantara – bayangkan gelombang tanap air; kedua, pengertian dasar eter ini berkaitan erat dengan gagasan Newton tentang ruang mutlak – eter dikaitkan sistem koordinat semesta agung. Dengan demikian, keuntungan sampingan yang akan diperoleh dari penyelidikan terhadap eter ini adalah bahwa dengan mengamati gerak bumi mengarungi eter, akan terungkap pula gerak bumi relatif terhadap “ruang mutlak”. Percobaan awal yang paling saksama untuk mendapatkan bukti kehadiran eter dilakukan pada tahun 1887 oleh fisikawan Amerika, Albert A. Michelson dan rekannya E.W. Morley. Mereka menggunakan interferometer Michelson.
Oleh karena itu, tidak mengherankan mengapa setelah segera setelah Maxwell memperlihatkan bahwa kehadiran gelombang elektromagnet diramalkan berdasarkan persamaan-persamaan elektromagnet klasik, para fisikawan segera melakukan berbagai upaya untuk mempelajari sifat zat perantara yang berperan bagi perambatan gelombang elektromagnet ini. Zat perantara ini disebut eter, namun karena zat ini belum pernah teramati dalam percobaan, maka dipostulatkan bahwa ia tidak bermassa dan tidak tampak, tetapi mengisi seluruh ruang, dan fungsi satu-satunya untuk merambatkan gelombang elektromagnet.
Konsep eter ini sangat menarik karena; pertama, sulit untuk membayangkan bagaimana sebuah gelombang dapat merambat tanpa memerlukan zat perantara – bayangkan gelombang tanap air; kedua, pengertian dasar eter ini berkaitan erat dengan gagasan Newton tentang ruang mutlak – eter dikaitkan sistem koordinat semesta agung. Dengan demikian, keuntungan sampingan yang akan diperoleh dari penyelidikan terhadap eter ini adalah bahwa dengan mengamati gerak bumi mengarungi eter, akan terungkap pula gerak bumi relatif terhadap “ruang mutlak”. Percobaan awal yang paling saksama untuk mendapatkan bukti kehadiran eter dilakukan pada tahun 1887 oleh fisikawan Amerika, Albert A. Michelson dan rekannya E.W. Morley. Mereka menggunakan interferometer Michelson.
Dalam
percobaan ini, seberkas cahaya monokromatik dipisahkan menjadi dua berkas yang
dibuat melewati dua lintasan berbeda dan kemudian diperpadukan kembali. Karena
adanya perbedaan panjang lintasan yang ditempuh kedua berkas, maka akan
dihasilkan suatu pola interferensi.
Anggaplah
interferometer pada gambar bergerak dari kanan ke kiri dengan kecepatan v
relatif terhadap eter. Kemudian relatif terhadap interferometer ada angin eter
dengan kecepatan ini dari kiri ke kanan. Kita mula-mula menghitung waktu t1
untuk cahaya, yaitu waktu yang dibutuhkan cahaya untuk menempuh jarak dari pengamat ke cermin A dan kembali ke pengamat,
dan waktu t2 adalah waktu untuk menempuh jarak dari pengamat ke
cermin B dan kembali, dan dianggap bahwa kecepatan cahaya relatif terhadap bumi
(dan di sini terhadap interferometer). Dalam alat Michelson-Morey kedua cermin
A dan B adalah tetap dalam posisi. Panjang L1 dan L2
adalah sama, maka:
L1 = L2 = L.
Jika
c adalah kecepatan cahaya yang relatif terhadap eter maka kecepatan sinar 1
relatif terhadap interferometer, bila sinar ini bergerak dari pengamat ke
cermin A adalah (c + v) dan waktu yang dibutuhkan adalah L/(c + v). Sinar yang
dipantulkan dari A merambat berlawanan arah dengan angin eter, kecepatannya
relatif terhadap interferometer adalah (c - v), dan waktu yang dibutuhkan untuk
menempuh jarak L adalah L/(c - v). Jumlah waktu untuk perjalanan keliling
adalah:
Lintasan
sinar 2, relatif terhadap interferometer, tegak lurus pada angin eter. Dalam
perjalanan dari pengamat ke B, sinar itu harus bergerak lambat menentang arus,
dengan kecepatan relatif terhadap eter. Resultan kecepatan ini dan kecepatan v
adalah tegak lurus pada angin eter dan besarnya adalah (c2 – v2)1/2.
Kecepatan ketika kembali adalah juga (c2 –
v2)1/2 dan waktu t2 untuk perjalanan
keliling adalah:
Perbedaan
waktu perjalanan untuk sinar 1 dan 2 adalah t1 –
t2 = ∆t, perbedaan lintasannya ∆x adalah
c∆t, sehingga:
Sekarang
umpamakan interferometer berputar 900 dari posisinya, atau sebesar
sudut sedemikian rupa sehingga angin eter pada diagram adalah vertikal. (Alat Michelson
dipasang pada dasar yang berat supaya stabil, dan terapung i atas air raksa
sehingga dapat bergerak dengan mudah). Maka sinar 1 dan 2 bertukar peranan dan
beda lintasan ∆x adalah:
Sebagai
akibat dari perputaran, beda lintasan berubah sebesar ∆x – ∆x'.
Perubahan satu panjang gelombang menyebabkan perubahan satu rumbai memotong
garis referensi bila dilihat dengan teleskop, sehingga perubahan rumbai yang
diharapkan ∆m adalah:
Jika
v kecil dibandingkan dengan c, maka perbandingan v2/c2
sangat kecil dan aproksimasi yag baik adalah:
Kemudian aproksimasi ini menjadi:
Umpama
kecepatan v adalah kecepatan orbit bumi mengelilingi matahari kira-kira 3 x 104
m/dt. Maka:
Dengan
memantulkan sinar 1 dan 2 bolak-balik beberapa kali, panjang L menjadi ekivalan
dengan 11 m. Perubahan rumbai yang diharapkan untuk panjang gelombang cahaya
hijau = 5,5 x 10-7 adalah:
atau
sebanyak empat sepersepuluh rumbai. Perubahan yang diiliki Michelson dan Morley
lebih kecil dari seperseratus rumbai, dan mereka berkesimpulan bahwa pada
kenyataannya, pada batas-batas penyelidikan yang tidak pasti ini, perubahan
adalah nol, dengan mengabaikan kecepatan orbit bumi yang nampakanya relatif
diam terhadap eter. Hasil ini merupakan teka-teki, dan masa kini penyelidikan
Michelson-Morey ini sangat berarti sebagai hasil negatif yang pernah didapat.
Berbagai
upaya dilakukan untuk menjelaskan hasil negatif dari eksperimen
Michelson-Morey, dan untuk menyelamatkan konsep kerangka eter dan transformasi
kecepatan Galileo untuk cahaya. Seluruh proposal yang dihasilkan dari
upaya-upaya ini telah dibuktikan salah. Tidak ada eksperimen dalam sejarah
fisika yang pernah sebegitu beraninya menjelaskan suatu ketiadaan hasil
penelitian yang diperkirakan seperti eksperimen Michelson-Morey. Einsteinlah
yang memecahkan persoalan tersebut pada tahun 1905 dengan teori relativitas
khusus yang digagasnya.

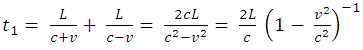








Post a Comment for "PERCOBAAN MICHELSON-MORLEY"
Sobat Fisika! Berikan Komentar di kolom komentar dengan bahasa yang sopan dan sesuai isi konten...Terimasih untuk kunjunganmu di blog ini, semoga bermanfaat!