Ketika sebuah partikel bergerak di dalam
lingkaran dengan laju konstan,
gerakannya disebut gerak melingkar beraturan
(uniform circular motion). Sebuah mobil
mengitari lengkungan dengan jari-jari konstan pada laju yang konstan, sebuah
satelit bergerak dalam orbit melingkar, dan seorang pemain ski es yang menari
dalam sebuah lingkaran dengan laju konstan, semuanya adalah contoh dari sebuah
gerak melingkar beraturan. Tidak ada komponen percepatan yang paralel
(percepatan tangensial) terhadap lintasan, bila ada lajunya akan berubah.
Komponen percepatannya tegak lurus (normal) terhadap lintasan yang menyebabkan
arah kecepatan berubah-ubah, berhubungan dengan laju partikel dan jari-jari
lingkaran.
Pada gerak melingkar beraturan
percepatannya tegak lurus terhadap kecepatan disetiap saat, karena arah
kecepatannya berubah maka arah percepatan juga berubah. Kita akan lihat bahwa
vektor percepatan di setiap titik di dalam lintasan lingkaran mengarah ke pusat
lingkaran.
 |
| Gambar 1: Mencari perubahan kecepatan dari pertikel yang bergerak melingkar beraturan. |
Gambar 1a memperlihatkan gerak partikel
dengan laju konstan di dalam sebuah lintasan lingkaran berjari-jari R yang
berpusat di O. Partikel bergerak dari P1
ke P2 selama ∆t. Perubahan vektor pada
kecepatan ∆v dalam waktu ini
diperlihatkan dalam gambar 1b.
Sudut yang diberi nama ∆φ pada gambar 1a adalah sama karena v1 tegak lurus pada garis OP1 dan v2 tegak lurus pada garis
OP2,
sehingga segitiga OP1P2 pada gambar 1a dan OP1P2 pada gambar 1b adalah serupa.
Perbandingan sisi yang bersesuaian adalah sama maka
besar percepatan rata-rata (arata-rata)
selama ∆t adalah
Besar a
dari percepatan sesaat a pada titik P1
adalah limit dari persamaan ini dengan mengambil titik P2 mendekati (sangat berimpit) dengan P1:
tetapi ∆s/∆t adalah laju v1 pada titik P1. Juga, P1 berupa titik
sembarang pada lintasan, maka kita dapat menghilangkan tanda 1-nya dan
membiarkan v mewakili laju pada sembarang titik. Sehingga
arah arad selalu mengarah
ke pusat lintasan melingkarnya. Vektor percepatan mengarah ke sisi
cekung dari lintasan melingkar sebuah partikel, yaitu mengarah ke dalam
lingkaran (tidak perna ke luar lingkaran). Karena laju konstanpercepatannya
selalu tegak lurus terhadap kecepatan sesaat. Hal ini diperlihatkan pada gambar
1c. Kita simpulkan: Dalam gerak melingkar
beraturan, besar a dari percepatan sesaat sama dengan kuadrat laju v dibagi jari-jari lingkaran R. Arahnya tegak lurus terhadap v dan berada di sepanjang jari-jari. Karena percepatannya selalu
mengarah ke pusat lingkaran seringkali disebut percepatan
sentripetal (centripetal acceleration).
Gambar 2 memperlihatkan arah vektor kecepatan dan percepatan pada beberapa
titik untuk partikel yang bergerak dalam gerak melingkar beraturan.
 |
| Gambar 2: Untuk sebuah partikel yang bergerak melingkar beraturan, kecepatan di setiap titik menyinggung lingkaran dan percepatannya mengarah ke pusat lingkaran. |
Kita juga dapat menyatakan besar dari
percepatan gerak melingkar beraturan dalam bentuk periode, T dari gerak, yaitu
waktu untuk satu putaran (saat pertikel mengelilingi lingkaran). Selama waktu T
partikel menempuh jarak yang sama dengan keliling lingkaran 2∏R, jadi
kecepatannya adalah
Jika kita
mensubtitusikan persamaan (2) ke persamaan (1), dan karena T = 1/f, dan v = Ωr, maka


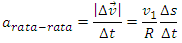




Post a Comment for "Gerak Melingkar Beraturan (Uniform circulation motion)"
Sobat Fisika! Berikan Komentar di kolom komentar dengan bahasa yang sopan dan sesuai isi konten...Terimasih untuk kunjunganmu di blog ini, semoga bermanfaat!