 |
| Gambar 1: Grafik yang menunjukkan (a) Pepindahan GHS, (b) kecepatan GHS dan (c) Percepatan GHS |
Gambar 1a, menunjukkan grafik perpindahan terhadap
waktu yang diberikan oleh persamaan x = A cos (ωt + φ). Kita dapat
menemukan kecepata v sebagai fungsi waktu dari grafik 2, besar dari v adalah vmaks sin Ө,
tetapi v mengarah ke kiri, sehingga v = - vmaks sin Ө. Lagi lagi dengan mengatur Ө
= ωt = 2∏ft = 2∏t/T kita
dapatkan
Hanya setelah t = 0, kecepatan negatif (mengarah ke kiri) dan tetap begitu
sampai t = ½ T (sesuai dengan Ө = 1800 = ∏ radian). Setelah t= ½ T sampai t
= T kecepatannya positif. Kecepatan sebagai fungsi waktu di atas diplot di
gambar 1b. Karena frekuensi gerak harmonik sederhana adalah f = 1/2∏ (k/m)1/2, maka
untuk sebuah sistem pegas massa tersebut,
laju maksimum vmaks lebih besar ketika
amplitudonya lebih besar, dan selalu terjadi saat massanya melewati titik
setimbang.
 |
| Gambar 2 |
Hukum II Newton memberi kita percepatan
sebagai fungsi waktu:
di mana percepatan maksimumnya adalah
Persamaan percepatan sebagai fungsi waktu
ini diplot pada gambar 1c. Karena percepatan GHS tidak konstan, persamaan untuk
gerak dipercepat beraturan tidak berlaku untuk GHS.


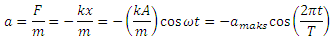

Post a Comment for "Kecepatan & Percepatan Gerak Harmonik Sederhana"
Sobat Fisika! Berikan Komentar di kolom komentar dengan bahasa yang sopan dan sesuai isi konten...Terimasih untuk kunjunganmu di blog ini, semoga bermanfaat!