Medan Magnet Sebuah Solenoida

Sebuah solenoida yang terdiri dari lilitan kawat yang berbentuk garis sekrup pada suatu silinder, biasanya mempunyai penampang lingkaran. Mungkin terdapat ratusan atau ribuan lilitan yang sangat rapat, yang masing-masing dapat dianggap sebagai kawat lingkaran berarus. Mungkin juga ada beberapa lapisan lilitan. Untuk sederhananya, gambar (1) yang memperlihatkan solenoida hanya dengan beberapa lilitan. Semua lilitan dilalui arus yang sama, dan medan magnet total B di tiap-tiap titik adalah jumlah vektor dari medan-medan magnet yang disebabkan oleh masing-masing lilitan. Gambar itu memperlihatkan garis-garis medan magnet dalam bidang xy.

Gambar (1): Garis-garis medan magnetik yang dihasilkan oleh arus dalam sebuah solenoida.

Garis-garis medan magnet di dekat pusat solenoida ini secara aproksimasi adalah paralel, yang menunjukkan sebuah medan B yang hampir homogen sedangkan di luar solenoida itu garis medan magnetiknya menyebar dan medan magnetiknya lemah. Jika solenoida leih panjang dibandingkan dengan diameter penampangnya dan koil-koil itu dililitkan secara ketat, maka medan internal di dekat titik tengah dari panjang solenoida sangat hampir homogen pada penampang solenoida dan paralel dengan sumbu solenoida, dan medan eksternal di dekat titik tengah itu sangat kecil.

Kita akan menggunakan hukum Ampere untuk mencari medan di pusat atau di dekat pusat sebuah solenoida panjang seperti ini. Solenoida ini memiliki n lilitan kawat per satuan panjang dan menghantar arus I.

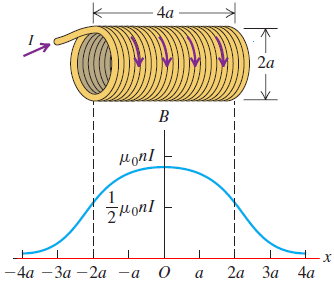
Gambar (2): Sebagian dari sebuah solenoida panjang yang diliit secara ketat yang berpusat pada usmbu x.

Kita memilih sebagai lintasan integrasi kita segiempat abcd dalam gambar (2). Sisi ab dengan panjang L, adalah paralel dengan sumbu solenoida, sisi bc dan sisi da diambil sangat panjang sehingga sisi cd jauh dari solenoida itu, maka medan magnet di sisi cd dapat diabaikan karena sangat kecil.

Karena simetri maka medan magnetik B sepanjang sisi ab adalah paralel dengan sisi ini dan besarnya konstan. Dalam menyelesaikan integrasi  hukum Ampere, kita mengikuti sisi ab dalam arah yang sama seperti B. Maka untuk sisi ini, BII = + B dan

Sepanjang sisi bc dan sisi da, BII = 0 karena B tegak lurus terhadap sisi-sisi ini. Sepanjang sisi cd, BII = 0 karena B = 0. Integral tetutup mengelilingi keleluruhan lintasan tertutup akan direduksi menjadi BL, yaitu

Banyaknya lilitan dalam panjang L adalah nL. Masing-masing lilitan ini lewat sekali melalui segiempat siku-siku abcd dan menghantar sebuah arus I, di mana I adalah arus dalam lilitan itu. Arus total yang dicakup oleh segi empat siku-siku itu adalah Iyang tercakup = nLI. Dari hukum Ampere, karena integral tertutup pada hukum Ampere positif, maka Iyang tercakup juga harus positif, maka arus yang lewat melalui permukaan yang dibatasi oleh lintasan integrasi itu harus berada dalam arah yang diperlihatkan pada gambar (2). Hukum Ampere kemudian memberi besar B:

Sisi ab tidak perlu terletak pada sumbu solenoida, sehingga perhitungan ini juga membuktikan bahwa medan ini homogen pada keseluruhan penampang di pusat dari panjangnya solenoida ini.

Untuk titik-titik sepanjang sumbu itu, medan magnetik paling kuat di pusat solenoida dan besarnya menurun di dekat ujung-ujung solenoida itu untuk sebuah solenoida yang sangat panjang dibandingkan dengan diameternya, medan magnetik di setiap ujung secara eksak adalah setengah dari kuatnya medan magnetik di pusat solenoida yaitu

Gambar (3) mempelihatkan sebuah grafik dari B sebagai fungsi x untuk titik-titik pada sumbu sebuah solenoida yang pendek.

Gambar (3): Besar medan magnet di setiap ujung solenoida kira-kira setengah dari nilainya di pusat solenoida.

Share :