Gambar di bawah ini memperlihatkan tampak atas dari sebuah CD yang
berputar. Keping cakram ini berputar pada sumbu O. Sumbu ini tegak lurus
terhadap bidang dari gambar 1.
Sebagai contoh, 600 sama dengan π/3 rad dan 450 sama dengan π/4 rad.
Oleh karena CD merupakan benda kaku jadi saat partikel CD bergerak sepanjang lingkaran dari garis acuan maka setiap partikel lainnya juga bergerak melalui sudut θ yang sama. Jadi, kita dapat menghubungkan sudut θ dengan seluruh benda kaku seperti halnya dengan sebuah partikel. Hal ini memungkinkan kita untuk mendefinisikan posisi sudut dari sebuah benda kaku pada saat melakukan gerak rotasi. Kita pilih sebuah garis acuannya berupa garis yang menghubungkan O dengan partikel tersebut. Posisi sudut benda kaku adalah sudut θ antara garis acuan dan garis yang sering disebut sumbu x. Cara yang sama dilakukan untuk mengidentifikasi posisi benda pada gerak translasi, jarak x antara benda dan posisi asal, x = 0.
Saat partikel pada benda kaku bergerak dari posisi A ke B selama interval waktu ∆t seperti gambar 2. Garis acuan dengan panjang r melalui sudut ∆θ = θf – θi. Besar ∆θ didefinisikan sebagai perpindahan sudut benda kaku:
 |
| Gambar 1: CD berotasi pada sumbu O |
Mari kita selidiki gerakan sala satu dari
jutaan partikel dari partikel penyusun CD. Sebuah partikel P berjarak r
dari pusat dan berputar dalam lingkaran berjari-jari r. (Sebenarnya,
seluruh partikel pada cakram mengalami gerak rotasi terhadap O). Akan
lebih mudah jika posisi P diwakili dengan koordinat polar/kutub (r, θ),
di mana r adalah jarak dari pusat ke P dan θ diukur berlawanan arah jarum jam dari
sebuah acuan garis acuan, seperti pada gambar. Dalam hal ini
satu-satunya koordinat partikel yang berubah seiring waktu adalah sudut
θ, sedangkan r tetap. Saat partikel bergerak memutar dari garis acuan (θ
= 0), ia bergerak melalui sebuah busur sepanjang s, seperti gambar.
Hubungan panjang busur s dan besar sudut θ adalah sebagai berikut
Perhatikan bahwa dimensi θ pada persamaan di atas adalah ratio dari
panjang busur dan jari-jari lingkaran, maka θ merupakan angka murni.
Meskipun demikian kita biasanya menyertakan satuan radian (rad) untuk θ, di manaSatu radian merupakan sudut yang dibentuk oleh panjang busur yang sama dengan jari-jari busur tersebut.Oleh karena keliling lingkaran adalah 2πr, maka persamaan sebelumnya sudut 3600 akan sama dengan (2πr/r) rad = 2π rad. (Perhatikan juga bahwa 2π rad sama dengan satu putaran penuh.) Oleh karena itu, 1 rad = 3600/2π ≅ 57,30. Untuk mengubah sebuah sudut dalam derajat menjadi radian, kita gunakan persamaan π rad = 1800, atau
Sebagai contoh, 600 sama dengan π/3 rad dan 450 sama dengan π/4 rad.
Oleh karena CD merupakan benda kaku jadi saat partikel CD bergerak sepanjang lingkaran dari garis acuan maka setiap partikel lainnya juga bergerak melalui sudut θ yang sama. Jadi, kita dapat menghubungkan sudut θ dengan seluruh benda kaku seperti halnya dengan sebuah partikel. Hal ini memungkinkan kita untuk mendefinisikan posisi sudut dari sebuah benda kaku pada saat melakukan gerak rotasi. Kita pilih sebuah garis acuannya berupa garis yang menghubungkan O dengan partikel tersebut. Posisi sudut benda kaku adalah sudut θ antara garis acuan dan garis yang sering disebut sumbu x. Cara yang sama dilakukan untuk mengidentifikasi posisi benda pada gerak translasi, jarak x antara benda dan posisi asal, x = 0.
Saat partikel pada benda kaku bergerak dari posisi A ke B selama interval waktu ∆t seperti gambar 2. Garis acuan dengan panjang r melalui sudut ∆θ = θf – θi. Besar ∆θ didefinisikan sebagai perpindahan sudut benda kaku:
∆θ = θf – θi
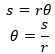

Post a Comment for "Posisi sudut "
Sobat Fisika! Berikan Komentar di kolom komentar dengan bahasa yang sopan dan sesuai isi konten...Terimasih untuk kunjunganmu di blog ini, semoga bermanfaat!