Pada lintasan lingkaran dalam model atom Bohr, besar momentum sudut
elektron adalah L = nℏ, di mana ℏ adalah (baca: h-bar) = h/2π dan h
adalah konstanta Planck. Menurut Schrodinger rumus di atas tidak
berlaku jika lintasan elektron berbentuk elips. Dengan menganggap
elektron berkelakuan seperti gelombang, Schrodinger menurunkan rumus
momentum sudut elektron:
Dengan l menyatakan bilangan kuantum orbital yang merupakan bilangan bulat dari 0 sampai n – 1 (n = bilangan kuantum utama).
l = 0, 1, 2, 3, . . . , n – 1
hasil perhitungan Schrodinger menunjukkan bahwa l berhubungan erat
dengan kepipihan elips lintasan elektron. Semakin kecil l semakin pipih
elips.Pada gambar di atas ditunjukkan lintasan elips untuk berbagai nilai l pada kulit n = 4. Jari-jari rata-rata elips (r = (a + b)/2, a = panjang sumbu mayor, b = panjang sumbu minor), dari keempat elips tersebut sama besar. Besar r ditentukan oleh bilangan kuantum n.
- Orbit dengan nilai l terbesar (l = n – 1) memiliki momentum sudut terbesar (momentum sudut diukur terhadap inti atom). Orbitnya berbentuk lingkaran.
- Semua nilai l yang lebih kecil akan memberikan elips yang lebih pipih.
- Pada l = 0 elips sangat pipih. Sumbu minor lintasan ini hampir sama dengan jari-jari inti atom. Jika inti atom dianggap titik, lintasan l = 0 berbentuk garis lurus. Ini sesuai dengan konsep momentum sudut di mana ketika L = 0, partikel bergerak lurus melewati titik awal.


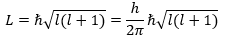
Post a Comment for "Bilangan Kuantum Orbital"
Sobat Fisika! Berikan Komentar di kolom komentar dengan bahasa yang sopan dan sesuai isi konten...Terimasih untuk kunjunganmu di blog ini, semoga bermanfaat!