Fakta bahwa pengamat dalam kerangka inersia yang berbeda selalu
mengukur interval waktu yang berbeda antara sepasang peristiwa dapat
diilustrasikan dengan cara lain dengan mempertimbangkan kendaraan
bergerak ke kanan dengan kecepatan v, seperti pada Gambar 1a.
Sebuah
cermin dipasang tetap di langit-langit kendaraan, dan pengamat O’, saat
diam dalam sistem ini, memegang laser pada jarak d di bawah cermin. Laser memancarkan pulsa cahaya yang diarahkan cermin (peristiwa 1), dan pada beberapa waktu kemudian, setelah dipantulkan dari cermin, pulsa cahaya tiba kembali di laser (peristiwa
2). Pengamat O‘ membawa jam C, yang ia gunakan untuk mengukur interval
waktu ∆t’ antara kedua peristiwa. Karena pulsa cahaya memiliki kecepatan
sebesar c, waktu yang dibutuhkan untuk perjalanan dari O’ ke cermin dan kembali lagi dapat ditemukan dari definisi kecepatan:
Interval waktu ∆t’, diukur oleh pengamat O’, yang membawa jam C dari kerangka acuan yang bergerak dengan kecepatan v.
Sekarang
perhatikan peristiwa yang sama seperti yang dilihat oleh pengamat O
dalam kerangka acuan kedua (Gambar. 1b). Menurut pengamat O (kerangka
acuan inersial/ kerangka acuan yang diam), cermin dan laser yang pindah
ke kanan dengan kecepatan v, dan sebagai hasilnya, urutan kejadian yang
muncul berbeda untuk Pengamat O. Pada saat cahaya dari laser mencapai
cermin, cermin telah pindah ke kanan jarak v∆t/2, di mana ∆t adalah
interval waktu yang diperlukan pulsa cahaya untuk berpindah dari O ke
cermin dan kembali yang diukur dengan O. Dengan kata lain, O
menyimpulkan bahwa, karena gerakan kendaraan, jika pulsa cahaya sampai
ke cermin, pulsa cahaya harus meninggalkan laser pada sudut tertentu
terhadap arah vertikal. Membandingkan gambar 1.a dan 1.b, kita
melihat bahwa cahaya melakukan perjalanan lebih jauh di (b) dari pada di
(a). (Perhatikan bahwa setiap pengamat tidak tahu bahwa dia sedang
bergerak. Setiap pengamat diam di dalam kerangka inersianya sendiri.)
 |
| Gambar 2 |
Menurut postulat kedua relativitas khusus, baik pengamat O dan O’ harus mengukur kecepatan cahaya c
yang sama. Karena cahaya berpindah lebih jauh menurut pengamat O, maka
∆t, interval waktu yang diukur oleh O lebih panjang dari interval waktu
∆t’ diukur oleh pengamat O’. Untuk mendapatkan hubungan antara ∆t dan
∆t’, lebih mudah menggunakan segitiga siku-siku yang ditunjukkan pada
gambar 2. Teorema phytagoras memberikan
Pecahkan untuk mendapatkan
Karena
Maka
di mana γ = (1 – v2/c2)-1/2. Karena
γ selalu lebih besar dari satu, jadi, menurut pengamat di O jam yang
ada di O’ tampak lebih lambat (seolah-olah waktu memuai atau mulur).
Efek ini dikenal sebagai dilasi waktu (pemuaian waktu). Interval waktu ∆t’ pada persamaan di atas disebut waktu yang sesungguhnya (proper time). Secara umum, waktu yang sesungguhnya, dilambangkan tp, didefinisikan sebagai
interval waktu antara dua Peristiwa yang diukur oleh pengamat yang
melihat peristiwa terjadi pada titik yang sama dalam ruang. Dalam kasus kami, pengamat O’ mengukur waktu yang tepat/sesungguhnya. Artinya, waktu yang tepat/sesungguhnya adalah waktu yang selalu diukur oleh pengamat bergerak bersama dengan jam. Maka persamaan di atas dapat ditulis sebagai
Dilasi
waktu adalah fenomena yang sangat nyata yang telah diverifikasi oleh
berbagai eksperimen. Misalnya, muon, partikel dasar yang tidak stabil
yang memiliki muatan sama dengan elektron dan massa 207 kali dari
elektron.
 |
| Gambar 3 |

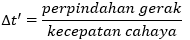


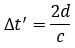


Post a Comment for "Dilasi waktu"
Sobat Fisika! Berikan Komentar di kolom komentar dengan bahasa yang sopan dan sesuai isi konten...Terimasih untuk kunjunganmu di blog ini, semoga bermanfaat!