Tidak hanya interval waktu antara dua peristiwa bergantung pada kerangka
acuan pengamat, tetapi jarak antara dua titik juga mungkin bergantung
pada kerangka acuan pengamat. Konsep simultanitas yang terlihat.
Misalnya Anda ingin mengukur panjang mobil yang bergerak. Salah satu
cara melakukannya adalah dengan memiliki dua asisten untuk membuat tanda
pada jalan yang beraspal di posisi bumper depan dan belakang. Kemudian
Anda mengukur jarak antara tanda tersebut. Tetapi asisten-asisten Anda
harus membuat tanda mereka pada waktu yang sama. Jika salah satu
menandai posisi bumper depan pada satu waktu dan tanda lainnya posisi
bumper belakang setengah detik kemudian, Anda tidak akan mendapatkan
panjang mobil yang sebenaranya. Karena kita telah mempelajari bahwa
simultanitas bukan merupakan suatu konsep yang mutlak, kita harus
melanjutkan dengan hati-hati. Untuk mengembangkan hubungan antara
panjang yang diukur sejajar dengan arah gerak dalam berbagai sistem
koordinat, kita menganggap eksperimen lain yang terpikirkan. Kita
memasang suatu sumber cahaya pada salah satu ujung penggaris dan cermin
pada ujung penggaris lainnya. Penggaris itu dalam keadaan diam dalam
kerangka acuan S’ dan panjangnya dalam kerangka ini adalah l0 (Gambar.1a).
Maka waktu ∆t’
yang dibutuhkan sebuah pulsa cahaya untuk melakukan perjalanan
pulang-pergi dari sumber ke cermin dan kembali ke sumber adalah
 |
| Gambar 1: (a) pulsa cahaya yang diukur oleh S' (Nadya) dan (b) pulsa cahaya yang diukur oleh S (Stephen) |
Ini
adalah interval waktu yang tepat karena keberangkatan dan kembali
terjadi pada saat yang sama di S’.Dalam kerangka acuan S penggaris
bergerak ke kanan dengan kecepatan u selama perjalanan dari pulsa cahaya itu(Gambar.1b). Panjang penggaris itu dalam S adalah l dan Waktu perjalanan dari sumber ke cermin, yang diukur dalam S, adalah ∆t1 bergerak sejauh u∆t1. Panjang total lintasan dari sumber ke cermin bukan l tetapi sama dengan
d = l + u∆t1
pulsa cahaya itu berjalan dengan laju c, sehingga benar juga bahwa
d = c∆t1
maka kita dapatkan bahwa
c∆t1 = l + u∆t1
atau
(dengan membagi jarak l dengan c – u tidak berari bahwa cahaya itu berjalan dengan laju c – u, tetapi hal itu berarti bahwa jarak yang ditempuh oleh pulsa itu dalam S lebih besar daripada l).Dengan cara yang sama kita dapat memperlihatkan bahwa waktu ∆t2 untuk perjalanan kembali dari cermin ke sumber adalahWaktu total ∆t = ∆t1 + ∆t2 untuk perjalanan pulang pergi, seperti yang diukur dalam S adalah
Kita juga mengetahui bahwa ∆t dan ∆t’ dihubungkan oleh persamaan ∆t = ∆t’/γ, karena ∆t’ adalah
waktu sesungguhnya (proper time)
dalam S’. Jadi waktu untuk perjalanan pulang pergi dalam kerangka diam
S’ dari penggaris itu menjadi
Akhirnya dengan menggabungkan kedua
persamaan terakhir untuk menghilangkan ∆t, kita peroleh
Jadi, panjang l yang diukur dalam S, di mana penggaris bergerak adalah lebih pendek daripada panjang l0 yang diukur dalam kerangka diamnnya S’. Catatan: ini
bukanlah suatu ilusi optis! Memang benar adanya bahwa penggaris itu
lebih pendek dalam kerangka acuan S daripada dalam kerangka diamnya S’. Sebuah panjang yang diukur dalam kerangka di mana benda itu diam dinamakan panjang sesungguhnya (proper time). Jadi l0 adalah panjang sesungguhnya dalam S’ dan panjang yang diukur dalam kerangka lain yang bergerak relatif terhadap S’ lebih kecil daripada l0. Efek ini dinamakan kontaksi panjang yang didefinisikan dalam persamaan terakhir di atas.





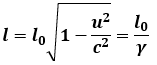
Post a Comment for "Kontraksi Panjang (length contaction)"
Sobat Fisika! Berikan Komentar di kolom komentar dengan bahasa yang sopan dan sesuai isi konten...Terimasih untuk kunjunganmu di blog ini, semoga bermanfaat!