Soal 1
Dua kabel digunakan untuk menopang massa 9,0 kg pada batang horisontal dengan panjang 2,1 m dan massa 21 kg seperti yang ditunjukkan pada gambar di bawah ini! Tentukan tegangan tali T!
Dua kabel digunakan untuk menopang massa 9,0 kg pada batang horisontal dengan panjang 2,1 m dan massa 21 kg seperti yang ditunjukkan pada gambar di bawah ini! Tentukan tegangan tali T!
Solusi:
Gambar gaya-gaya yang bekerja pada batang ditunjukkan pada gambar di bawah ini
Dengan mengambil poros sistem di titik O (ujung kiri batang), maka
ΣτO = 0
T(2,1 m) – (90 N)(1,05 m) – (210 N)(1,2 m) = 0
T(2,1 m) = 94,5 Nm + 252 Nm = 346,5 Nm
T = 165 N
Soal 2
Salah satu ujung sebuah tongkat homogen (massa m dan panjang tali L), tergantung dengan menggunakan tali dan ujung tongkat lainnya bersentuhan dengan lantai dalam keadaan diam. Tongkat tersebut membentuk sudut θ terhadap horisontal. Tentukan gaya tegangan tali!
Ambil poros di titik A, maka gaya normal pada A (NA) tidak menyebabkan torsi. Sehingga hanya gaya berat tongkat w, dan gaya tegangan tali T yang menyebabkan torsi pada A. Lengan momen untuk masing-masing gaya diukur dari poros A adalah
Gaya w, lengan momennya à AC’ = ½ L cos θ
Gaya T, lengan momennya à AB’ = L cos θ
Maka resultan momen gaya pada titik A adalah
ΣτA = 0
(w x ½ L cos θ) – (T x L cos θ) = 0
T = ½mg
Soal 3
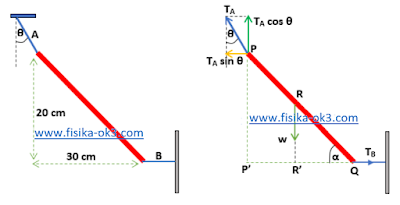
Batang homogen bermassa m diikat dengan tali A dan B setimbang pada posisi seperti pada gambar di bawah ini, dengan tali B horisontal. Tentukan nilai tan θ.
Dengan mengambil poros sistem di titik O (ujung kiri batang), maka
ΣτO = 0
T(2,1 m) – (90 N)(1,05 m) – (210 N)(1,2 m) = 0
T(2,1 m) = 94,5 Nm + 252 Nm = 346,5 Nm
T = 165 N
Soal 2
Salah satu ujung sebuah tongkat homogen (massa m dan panjang tali L), tergantung dengan menggunakan tali dan ujung tongkat lainnya bersentuhan dengan lantai dalam keadaan diam. Tongkat tersebut membentuk sudut θ terhadap horisontal. Tentukan gaya tegangan tali!
Solusi:
Ambil poros di titik A, maka gaya normal pada A (NA) tidak menyebabkan torsi. Sehingga hanya gaya berat tongkat w, dan gaya tegangan tali T yang menyebabkan torsi pada A. Lengan momen untuk masing-masing gaya diukur dari poros A adalah
Gaya w, lengan momennya à AC’ = ½ L cos θ
Gaya T, lengan momennya à AB’ = L cos θ
Maka resultan momen gaya pada titik A adalah
ΣτA = 0
(w x ½ L cos θ) – (T x L cos θ) = 0
T = ½mg
Soal 3
Batang homogen bermassa m diikat dengan tali A dan B setimbang pada posisi seperti pada gambar di bawah ini, dengan tali B horisontal. Tentukan nilai tan θ.
Jawab:
Ambil poros di titik P, maka gaya tegangan tali pada P (TA) tidak menyebabkan torsi. Sehingga hanya gaya berat tongkat w, dan gaya tegangan tali T yang menyebabkan torsi pada A. Lengan momen untuk masing-masing gaya diukur dari poros A adalah
→ resultan gaya-gaya pada sumbu-x
ΣFx = 0
TB – TA sin θ = 0 à TB = TA sin θ (1)
→ resultan gaya-gaya pada sumbu-y
ΣFy = 0
TA cos θ – w = 0 à w = TA cos θ (2)
→ rotasi terhadap titik P
Poros di titik P, maka resultan momen gaya pada P adalah
ΣτP = 0
TB x PP’ + (– w x QR’) = 0
TB L sin α + (– w x ½ L cos α) = 0
TB = ½ w cot α (3)
Bagi persamaan (1) dan (2) kita peroleh
(TA sin θ)/(TA cos θ) = TB/w
tan θ = TB/w (4)
Subtitusi (3) ke (4) kita peroleh
tan θ = (½ w cot α)/w
tan θ = ½ cot α
karena nilai cot α = 30 cm /20 cm = 3/2, maka
tan θ = 3/4
Soal 4
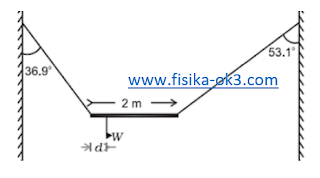
Sebuah batang homogen dengan berat W digantung pada dua utas tali yang massanya diabaikan seperti terlihat pada gambar di bawah ini! Tentukan pusat massa batang (pusat gravitasi) d dari ujung kiri batang!
Ambil poros di titik P, maka gaya tegangan tali pada P (TA) tidak menyebabkan torsi. Sehingga hanya gaya berat tongkat w, dan gaya tegangan tali T yang menyebabkan torsi pada A. Lengan momen untuk masing-masing gaya diukur dari poros A adalah
→ resultan gaya-gaya pada sumbu-x
ΣFx = 0
TB – TA sin θ = 0 à TB = TA sin θ (1)
→ resultan gaya-gaya pada sumbu-y
ΣFy = 0
TA cos θ – w = 0 à w = TA cos θ (2)
→ rotasi terhadap titik P
Poros di titik P, maka resultan momen gaya pada P adalah
ΣτP = 0
TB x PP’ + (– w x QR’) = 0
TB L sin α + (– w x ½ L cos α) = 0
TB = ½ w cot α (3)
Bagi persamaan (1) dan (2) kita peroleh
(TA sin θ)/(TA cos θ) = TB/w
tan θ = TB/w (4)
Subtitusi (3) ke (4) kita peroleh
tan θ = (½ w cot α)/w
tan θ = ½ cot α
karena nilai cot α = 30 cm /20 cm = 3/2, maka
tan θ = 3/4
Soal 4
Sebuah batang homogen dengan berat W digantung pada dua utas tali yang massanya diabaikan seperti terlihat pada gambar di bawah ini! Tentukan pusat massa batang (pusat gravitasi) d dari ujung kiri batang!
Jawab:
panjang batang, l
= 2 m
T1 dan T2 adalah gaya tegangan tali yang dihasilkan akibat berat batang.
Keseimbangan statis memberikan:
T1 Sin 36.90 = T2 Sin 53.10
T1 / T2 = 4 / 3
⇒ T1 = (4/3) T2
Untuk keseimbangan rotasi dengan poros di pusat berat batang:
T1 (Cos 36.9) × d = T2 Cos 53.1 (2 - d)
T1 × 0.800 d = T2 × 0.600 (2 - d)
(4/3) × T2 × 0.800d = T2 (0.600 × 2 - 0.600d)
1.067d + 0.6d = 1.2
∴ d = 1.2 / 1.67
= 0.72 m
oleh karena itu pusat gravitasi dari batang 0,72 m dari ujung kiri batang.
T1 dan T2 adalah gaya tegangan tali yang dihasilkan akibat berat batang.
Keseimbangan statis memberikan:
T1 Sin 36.90 = T2 Sin 53.10
T1 / T2 = 4 / 3
⇒ T1 = (4/3) T2
Untuk keseimbangan rotasi dengan poros di pusat berat batang:
T1 (Cos 36.9) × d = T2 Cos 53.1 (2 - d)
T1 × 0.800 d = T2 × 0.600 (2 - d)
(4/3) × T2 × 0.800d = T2 (0.600 × 2 - 0.600d)
1.067d + 0.6d = 1.2
∴ d = 1.2 / 1.67
= 0.72 m
oleh karena itu pusat gravitasi dari batang 0,72 m dari ujung kiri batang.




Post a Comment for "Soal kesetimbangan benda tegar dan penyelesaiannya"
Sobat Fisika! Berikan Komentar di kolom komentar dengan bahasa yang sopan dan sesuai isi konten...Terimasih untuk kunjunganmu di blog ini, semoga bermanfaat!