Soal 1
Dua bidang H dan V saling tegak lurus. Pada kedua bidang tersebut terdapat kawat panjang yang masing-masing dialiri arus 4 A dan 6 A. Hitung besar kuat medan magnaetik di titik O (lihat gambar).
Jawab:
Arus i1 menimbulkan medan magnetik B1 yang arahnya ke arah sumbu X (gunakan aturan tangan kanan), sedangkan arus i2 menimbulkan medan magnetik B2 yang arahnya ke arah sumbu Y.
B1 = μ0i1/2πa1 = (4π x 10-7).4/(2π.0,04) = 2 x 10-5 T (arah lihat gambar)
Medan magnetik akibat arus i2 = 6 A (di mana a2 = 8 cm = 0,08 m)
B1 = μ0i1/2πa1 = (4π x 10-7).6/(2π.0,08) = 1,5 x 10-5 T (arah lihat gambar)
Medan magnetik total:
B = (B12 + B22)1/2 = 10-5(22 + 1,52)1/2
B = 2,5 x 10-5 T
Soal 2
Dua kawat panjang berjarak 10 cm masing-masing membawa arus 2,6 A dan 3,9 A. Berapakah besar kuat medan magnetik di titik P?
Jawab:
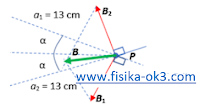
Medan magnetik yang dihasilkan oleh masing-masing kawat digambarkan pada gambar di bawah.
a1 = (52 + 122)1/2 = 13 cm = 0,13 m dan a2 = a1 = 0,13 m
maka
B1 = μ0i1/2πa1 = (4π x 10-7)(2,6)/(2π.0,13) = 4 x 10-6 T (arah lihat gambar) dan
B2 = μ0i2/2πa2 = (4π x 10-7)(3,9)/(2π.0,13) = 6 x 10-6 T (arah lihat gambar)
Perhatikan gambar di bawah ini
tan α = 5/12 maka α = 22,620, maka
B = [B12 + B22 + 2B1B2 cos α]1/2
= 10-6[(4)2 + (6)2 + 2(4)(6) cos 22,620]1/2
B = 4,27 x 10-6 T
Soal 3
Dua kawat a dan b lurus dan panjang terletak sejajar dan berjarak 10 cm, masing-masing 4 A (pada arah yang sama). Hitung besar kuat medan magnetik di sebuah titik yang berjarak 6 cm dari a dan 8 cm dari b!
Jawab:
Arah medan magnetik yang disebabkan kedua arus digambarkan seperti di bawah. Resultan dapat dicari dengan rumus vektor.
Medan magnetik akibat arus a (Ia = 4 A, aa = 6 cm = 0,06 m)
Ba = μ0ia/2πaa = (4π x 10-7)(4)/(2π.0,06) = 1,33 x 10-5 T
Medan magnetik akibat arus B (IB = 4 A, aa = 6 cm = 0,08 m)
Ba = μ0ia/2πaa = (4π x 10-7)(4)/(2π.0,08) = 10-5 T
Maka medan magnetik total adalah
B = (Bx2 + By2)1/2
B = 10-5 [(4/3)2 + (1)2]1/2 = 1,67 x 10-5 T
Soal 4
Kawat bujur sangkar ABCD dialiri arus 2 A. Hitung kuat medan magnetik dipusat bujur sangkar tersebut! (sisi bujur sangkar 2 cm)
Jawab:
Anggap sisi bujur sangkar b. Kuat medan magnetik oleh kawat yang tidak panjang adalah
B = (μ0i/4πa)(cos θ1 – cos θ2)
Yang menjadi masalah dalam soal ini adalah menentukan θ1 dan θ2. Konstribusi kawat AB: (θ1 = 450, θ2 = 1350)
BAB = (μ0i/4πa)(cos 450 – cos 1350)
= [μ0i/4π(b/2)][√2/2 – (√2/2)]
BAB = μ0i√2/2πb
Dapat dibuktikan bahwa dengan aturan tangan kanan bahwa kontribusi medan magnetik dari kawat BC, CD dan DA arahnya sama dengan arah medan magnetik dari kawat AB dan juga kontribusi masing-masing kawat sama besar.
Jadi kuat medan magnetik di pusat bujur sangkar adalah
B = 4BAB = 4(μ0i√2/2πb)
B = 2μ0i√2/πb
Maka dengan i = 2 A dan b = 2 cm = 0,02 m kita dapatkan
B = 2(4π x 10-7)(2)√2/(π. 0,02) = 1,13 x 10-4 T
Soal 5
Tiga kawat panjang P, Q dan R disusun seperti pada gambar (i). IQ = IP = 2 A dan IR = 4 A, jarak PQ = QR = 10 cm. Carilah titik pada garis PR yang kuat medan magnetiknya nol!
Jawab: Misalnya titik yang dimaksud berjarak x dari P. Anggap BP, BQ dan BR merupakan kuat medan magnetik untuk masing-masing kawat P, Q, dan R (arahnya dicari pakai aturan tangan kanan dan diberikan pada gambar)
Agar kuat medan magnetik di titik tersebut nol maka
BQ = BP + BR
μ0iQ/2πaQ = μ0iP/2πaP + μ0iR/2πaR
IQ/aQ = IP/aP + IR/aR
2/(0,1 – x) = 2/x + 4/(0,2 – x)
2x(0,2 – x) = [2(0,2 – x) + 4x](0,1 – x)
0,4x = 0,04 – 0,2x
0,6x = 0,04
x = 1/15 cm
Dua bidang H dan V saling tegak lurus. Pada kedua bidang tersebut terdapat kawat panjang yang masing-masing dialiri arus 4 A dan 6 A. Hitung besar kuat medan magnaetik di titik O (lihat gambar).
Jawab:
Arus i1 menimbulkan medan magnetik B1 yang arahnya ke arah sumbu X (gunakan aturan tangan kanan), sedangkan arus i2 menimbulkan medan magnetik B2 yang arahnya ke arah sumbu Y.
Kuat medan magnetik total dapat dicari dengan menjumlahkan secara vektor medan magnetik B1 dan B2.
Medan magnetik akibat arus i1 = 4 A (di mana a1 = 4 cm = 0,04 m)B1 = μ0i1/2πa1 = (4π x 10-7).4/(2π.0,04) = 2 x 10-5 T (arah lihat gambar)
Medan magnetik akibat arus i2 = 6 A (di mana a2 = 8 cm = 0,08 m)
B1 = μ0i1/2πa1 = (4π x 10-7).6/(2π.0,08) = 1,5 x 10-5 T (arah lihat gambar)
Medan magnetik total:
B = (B12 + B22)1/2 = 10-5(22 + 1,52)1/2
B = 2,5 x 10-5 T
Soal 2
Dua kawat panjang berjarak 10 cm masing-masing membawa arus 2,6 A dan 3,9 A. Berapakah besar kuat medan magnetik di titik P?
Jawab:
Medan magnetik yang dihasilkan oleh masing-masing kawat digambarkan pada gambar di bawah.
Medan magnetik total dapat dicari dengan menggunakan rumus penjumlahan vektor. Dengan
Kuat arus i1 = 2,6 A dan i2 = 3,9 A,a1 = (52 + 122)1/2 = 13 cm = 0,13 m dan a2 = a1 = 0,13 m
maka
B1 = μ0i1/2πa1 = (4π x 10-7)(2,6)/(2π.0,13) = 4 x 10-6 T (arah lihat gambar) dan
B2 = μ0i2/2πa2 = (4π x 10-7)(3,9)/(2π.0,13) = 6 x 10-6 T (arah lihat gambar)
Perhatikan gambar di bawah ini
tan α = 5/12 maka α = 22,620, maka
B = [B12 + B22 + 2B1B2 cos α]1/2
= 10-6[(4)2 + (6)2 + 2(4)(6) cos 22,620]1/2
B = 4,27 x 10-6 T
Soal 3
Dua kawat a dan b lurus dan panjang terletak sejajar dan berjarak 10 cm, masing-masing 4 A (pada arah yang sama). Hitung besar kuat medan magnetik di sebuah titik yang berjarak 6 cm dari a dan 8 cm dari b!
Jawab:
Arah medan magnetik yang disebabkan kedua arus digambarkan seperti di bawah. Resultan dapat dicari dengan rumus vektor.
Medan magnetik akibat arus a (Ia = 4 A, aa = 6 cm = 0,06 m)
Ba = μ0ia/2πaa = (4π x 10-7)(4)/(2π.0,06) = 1,33 x 10-5 T
Medan magnetik akibat arus B (IB = 4 A, aa = 6 cm = 0,08 m)
Ba = μ0ia/2πaa = (4π x 10-7)(4)/(2π.0,08) = 10-5 T
B = (Bx2 + By2)1/2
B = 10-5 [(4/3)2 + (1)2]1/2 = 1,67 x 10-5 T
Soal 4
Kawat bujur sangkar ABCD dialiri arus 2 A. Hitung kuat medan magnetik dipusat bujur sangkar tersebut! (sisi bujur sangkar 2 cm)
Anggap sisi bujur sangkar b. Kuat medan magnetik oleh kawat yang tidak panjang adalah
B = (μ0i/4πa)(cos θ1 – cos θ2)
Yang menjadi masalah dalam soal ini adalah menentukan θ1 dan θ2. Konstribusi kawat AB: (θ1 = 450, θ2 = 1350)
BAB = (μ0i/4πa)(cos 450 – cos 1350)
= [μ0i/4π(b/2)][√2/2 – (√2/2)]
BAB = μ0i√2/2πb
Dapat dibuktikan bahwa dengan aturan tangan kanan bahwa kontribusi medan magnetik dari kawat BC, CD dan DA arahnya sama dengan arah medan magnetik dari kawat AB dan juga kontribusi masing-masing kawat sama besar.
Jadi kuat medan magnetik di pusat bujur sangkar adalah
B = 4BAB = 4(μ0i√2/2πb)
B = 2μ0i√2/πb
Maka dengan i = 2 A dan b = 2 cm = 0,02 m kita dapatkan
B = 2(4π x 10-7)(2)√2/(π. 0,02) = 1,13 x 10-4 T
Soal 5
Tiga kawat panjang P, Q dan R disusun seperti pada gambar (i). IQ = IP = 2 A dan IR = 4 A, jarak PQ = QR = 10 cm. Carilah titik pada garis PR yang kuat medan magnetiknya nol!
Jawab: Misalnya titik yang dimaksud berjarak x dari P. Anggap BP, BQ dan BR merupakan kuat medan magnetik untuk masing-masing kawat P, Q, dan R (arahnya dicari pakai aturan tangan kanan dan diberikan pada gambar)
Agar kuat medan magnetik di titik tersebut nol maka
BQ = BP + BR
μ0iQ/2πaQ = μ0iP/2πaP + μ0iR/2πaR
IQ/aQ = IP/aP + IR/aR
2/(0,1 – x) = 2/x + 4/(0,2 – x)
2x(0,2 – x) = [2(0,2 – x) + 4x](0,1 – x)
0,4x = 0,04 – 0,2x
0,6x = 0,04
x = 1/15 cm





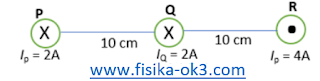

Post a Comment for "Soal Medan Magnet pada Kawat Lurus dan Pembahasannya"
Sobat Fisika! Berikan Komentar di kolom komentar dengan bahasa yang sopan dan sesuai isi konten...Terimasih untuk kunjunganmu di blog ini, semoga bermanfaat!