Soal 1
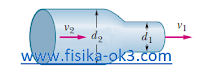
Perhatikan gambar!
Solusi:
(a) persamaan kontinuitas, A1v1 = A2v2 = Q = V/t
¼ πd12 v1= V/t
Perhatikan gambar!
Jika diameter penampang besar 5 cm dan diameter penampang kecil 3 cm, kecepatan aliran fluida pada pipa kecil v1 =
15 m/s. Tentukan: (a) berapa volume air yang mengalir pada kedua
penampang selama 10 menit, (b) besar kecepatan pada penampang besar v2 dan (c) tekanan gauge dalam penampang?
Solusi:
(a) persamaan kontinuitas, A1v1 = A2v2 = Q = V/t
¼ πd12 v1= V/t
¼ π (0,03 m)2 (15 m/s) = (V/600 s)
V = 6,4 m3
(b) dengan menggunakan persamaan kontinuitas, v1A1 = v2A2, karena A1 = ¼ πd2, maka
v1d12 = v2d22
(15 m/s)(3 cm)2 = v2 (5 cm)2
v2 = 5,4 m/s
(c) tekanan gauge adalah perbedaan tekanan dalam pipa horisontal tersebut yaitu,
P1 – P2 = ½ ρ(v12 – v22) = ½ (1000 kg/m3){(15 m/s)2 – (5,4 m/s)2} = 97920 Pa
Soal 2
Posisi pipa besar adalah 6 m diatas tanah dan pipa kecil 1 m diatas tanah. Kecepatan aliran air pada pipa besar adalah 72 km/jam dengan tekanan 25,5 x 105 Pa. Jika perbandingan luas A1 : A2 = 3 : 1, tentukan :
(a) Kecepatan air pada pipa kecil
(b) Selisih tekanan pada kedua pipa
(c) Tekanan pada pipa kecil
(ρair = 1000 kg/m3)
Solusi
h1 = 6 m
h2 = 1 m
v1 = 72 km/jam = 20 m/s
P1 = 5,5 x 105 Pa
A1 : A2 = 3 : 1
a) Kecepatan air pada pipa kecil
Persamaan Kontinuitas :
A1v1 = A2v2
(3)(20) = (1) (v2)
v2 = 60 m/s
b) Selisih tekanan pada kedua pipa
Dari Persamaan Bernoulli :
P1 + 1/2 ρv12 + ρgh1 = P2 + 1/2 ρv22 + ρgh2
P1 − P2 = 1/2 ρ(v22 − v12) + ρg(h2 − h1)
P1 − P2 = 1/2(1000)(602 − 202) + (1000)(10)(1 − 6)
P1 − P2 = (500)(3200) − 50000 = 1600000 − 50000
P1 − P2 = 1550000 Pa = 1,55 x 106 Pa
c) Tekanan pada pipa kecil
P1 − P2 = 1,55 x 106
2,55 x 106 − P2 = 1,55 x 106
P2 = 1,0 x 106 Pa
V = 6,4 m3
(b) dengan menggunakan persamaan kontinuitas, v1A1 = v2A2, karena A1 = ¼ πd2, maka
v1d12 = v2d22
(15 m/s)(3 cm)2 = v2 (5 cm)2
v2 = 5,4 m/s
(c) tekanan gauge adalah perbedaan tekanan dalam pipa horisontal tersebut yaitu,
P1 – P2 = ½ ρ(v12 – v22) = ½ (1000 kg/m3){(15 m/s)2 – (5,4 m/s)2} = 97920 Pa
Soal 2
Posisi pipa besar adalah 6 m diatas tanah dan pipa kecil 1 m diatas tanah. Kecepatan aliran air pada pipa besar adalah 72 km/jam dengan tekanan 25,5 x 105 Pa. Jika perbandingan luas A1 : A2 = 3 : 1, tentukan :
(a) Kecepatan air pada pipa kecil
(b) Selisih tekanan pada kedua pipa
(c) Tekanan pada pipa kecil
(ρair = 1000 kg/m3)
h1 = 6 m
h2 = 1 m
v1 = 72 km/jam = 20 m/s
P1 = 5,5 x 105 Pa
A1 : A2 = 3 : 1
a) Kecepatan air pada pipa kecil
Persamaan Kontinuitas :
A1v1 = A2v2
(3)(20) = (1) (v2)
v2 = 60 m/s
b) Selisih tekanan pada kedua pipa
Dari Persamaan Bernoulli :
P1 + 1/2 ρv12 + ρgh1 = P2 + 1/2 ρv22 + ρgh2
P1 − P2 = 1/2 ρ(v22 − v12) + ρg(h2 − h1)
P1 − P2 = 1/2(1000)(602 − 202) + (1000)(10)(1 − 6)
P1 − P2 = (500)(3200) − 50000 = 1600000 − 50000
P1 − P2 = 1550000 Pa = 1,55 x 106 Pa
c) Tekanan pada pipa kecil
P1 − P2 = 1,55 x 106
2,55 x 106 − P2 = 1,55 x 106
P2 = 1,0 x 106 Pa
Soal 3
Air mengalir ke bawah melalui suatu pipa seperi pada gambar dengan laju alir 15 L/s. Jika air memasuki ujung pipa 2 dengan kelajuan 5,0 m/s, berapa beda tekanan di antara kedua ujung pipa tersebut, jika h = 1,5 m dan luas penampang pipa besar A1 = 10 cm2.
h2 = 6 m
h1 = 0
v2 = 5 m/s
A1 = 10 cm2
Q = 15 L/s = 1,5 x 10-2 m3/s
maka Q = v2A2 à A2 = (1,5 x 10-2 m3/s)/(5,0 m/s) = 0,3 x 10-2 m2 = 30 cm2
dan Q = v1A1 à v1 = (1,5 x 10-2 m3/s)/(0,1 x 10-2 m2) = 15 m/s
Selisih tekanan pada kedua pipa
Dari Persamaan Bernoulli :
P1 + 1/2 ρv12 + ρgh1 = P2 + 1/2 ρv22 + ρgh2
P2 – P1 = 1/2 ρ(v12 − v12) + ρg(h1 – h2)
P2 − P1 = 1/2(1000)(252 − 52) + (1000)(10)(0 – 1,5)
P2 – P1 = (500)(600) – 15000 = 300000 − 15000
P2 – P1 = 285000 Pa = 285 kPa
Soal 4
Sebuah pipa pancur memiliki mulut pipa 2 cm. Pancuran didesain untuk dapat memancarkan air secara vertikal ke atas setinggi 20 m dari permukaan tanah. Pipa pancur dihubungkan ke permukaan air yang terletak 5 m di bawah tanah. Bila diameter mulut pompa 4 cm. Berapakah tekanan pompa harus didesain?
Jawab:
pipa yang lebih lebar (indeks 1) dan pipa yang kecil (indeks 2), berlaku hukum kontinuitas,
v1A1 = v2A2
v1d12 = v2d22, maka
v1/v2 = (d2/d1)2 = (2/4)2 = ¼
v2 = 4v1
air keluar dari pipa sempit (d2) dengan kecepatan v2 dan semburan naik setinggi 20 m, maka berlaku
½ mv22 = mgh
½ v22 = 10 kg/m2 x 20 m
v2 = 20 m/s, maka
v1 = v2/4 = 5 m/s
Sehingga dengan menggunakan persamaan Bernoulli kita peroleh,
P1 + ½ρv12 + ρgh1 = P2 + ½ρv22 + ρgh2
Ppompa + ½ (1000 kg/m3)(5 m/s)2 + 0 = 100 kPa + ½ (1000 kg/m3)(20 m/s)2 + (1000 kg/m3)(10 m/s2)(5 m)
Ppompa + 12,5 kPa = 100 kPa + 200 kPa + 50 kPa
Ppompa = 337,5 kPa
Jadi, agar air dapat keluar dari pancuran setinggi 20 m maka pompa yang dipakai minimal menghasilkan tekanan sebesar 337,5 kPa.
Sebuah pipa pancur memiliki mulut pipa 2 cm. Pancuran didesain untuk dapat memancarkan air secara vertikal ke atas setinggi 20 m dari permukaan tanah. Pipa pancur dihubungkan ke permukaan air yang terletak 5 m di bawah tanah. Bila diameter mulut pompa 4 cm. Berapakah tekanan pompa harus didesain?
pipa yang lebih lebar (indeks 1) dan pipa yang kecil (indeks 2), berlaku hukum kontinuitas,
v1A1 = v2A2
v1d12 = v2d22, maka
v1/v2 = (d2/d1)2 = (2/4)2 = ¼
v2 = 4v1
air keluar dari pipa sempit (d2) dengan kecepatan v2 dan semburan naik setinggi 20 m, maka berlaku
½ mv22 = mgh
½ v22 = 10 kg/m2 x 20 m
v2 = 20 m/s, maka
v1 = v2/4 = 5 m/s
Sehingga dengan menggunakan persamaan Bernoulli kita peroleh,
P1 + ½ρv12 + ρgh1 = P2 + ½ρv22 + ρgh2
Ppompa + ½ (1000 kg/m3)(5 m/s)2 + 0 = 100 kPa + ½ (1000 kg/m3)(20 m/s)2 + (1000 kg/m3)(10 m/s2)(5 m)
Ppompa + 12,5 kPa = 100 kPa + 200 kPa + 50 kPa
Ppompa = 337,5 kPa
Jadi, agar air dapat keluar dari pancuran setinggi 20 m maka pompa yang dipakai minimal menghasilkan tekanan sebesar 337,5 kPa.
Post a Comment for "Soal Asas Bernoulli dan Pembahasan"
Sobat Fisika! Berikan Komentar di kolom komentar dengan bahasa yang sopan dan sesuai isi konten...Terimasih untuk kunjunganmu di blog ini, semoga bermanfaat!