Soal Grafik Posisi, Kecepatan dan Percepatan pada Gerak Lurus dan Pembahasan

Soal 1
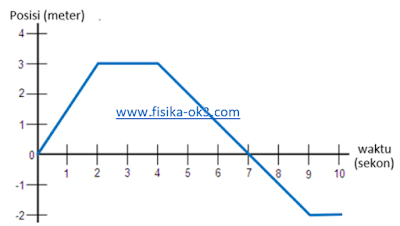
Posisi benda selama interval waktu 10 detik ditunjukkan oleh grafik di bawah ini:

(a) Tentukan jarak total dan perpindahan benda.
(b) Berapa kecepatan benda pada waktu-waktu berikut: t = 1, t = 3, dan t = 6.
(c) Tentukan kecepatan rata-rata benda dan kecepatan rata-rata dari t = 0 hingga t = 10.
(d) Berapakah percepatan benda pada t = 5?

Jawab:
(a) Jarak total yang ditempuh oleh benda adalah jumlah dari semua jarak yang ditempuh selama interval waktu. Dalam dua detik pertama, bergerak sejauh 3 m. Kemudian ia menempuh perjalanan 0 m dalam dua detik berikutnya. Kemudian selama lima detik berikutnya, benda bergerak sejauh 5 m, kemudian benda diam. jadi jarak totalnya adalah 3 + 5 = 8 m.
Perpindahan benda hanyalah posisi akhir dikurangi posisi awal, atau -2 - 0 = -2 m.
(b) Perhatikan bahwa setiap titik ini berada di tengah-tengah segmen garis pada grafik. Karena ini, kecepatan sesaat pada titik-titik ini sama dengan kecepatan rata-rata selama interval waktu yang diwakili oleh setiap segmen, jadi:

v(t) = (x₂ – x₁)/(t₂ – t₁)
v(1) = (3 – 0)/(2 – 0) = 3/2 = 1,5 m / s
v(3) = (3 – 3)/(4 – 2) = 0/2 = 0 m / s
v(6) = (-2 – 3)/(9 – 4) = -5/5 = -1 m / s

Perhatikan: bahwa rumus (x₂ – x₁)/(t₂ – t₁) sama dengan rumus kemiringan untuk grafik ini. Kecepatan pada titik mana pun pada grafik posisi vs waktu hanyalah kemiringan grafik pada titik tersebut.

Dengan definisi ini, kita juga tahu bahwa kecepatan dari setiap fungsi posisi adalah turunannya terhadap waktu. Anda juga dapat beralih dari fungsi kecepatan ke fungsi posisi menggunakan integral.

(c) Kecepatan rata-rata adalah perpindahan dibagi waktu. Kami menemukan sebagian bahwa perpindahan objek adalah -2 m, jadi:
v_rata-rata = -2/10 = -0,2 m/s

Kelajuan rata-rata adalah jarak total yang dibagi menjadi waktu, dan kami menemukan sebagian bahwa jarak total objek yang ditempuh adalah 8 m. Jadi:
Kelajuan rata-rata = 8/10 = 0,8 m/dtk

(d) Kita telah menemukan di bagian b bahwa kecepatan benda diwakili oleh kemiringan garis segmen pada grafik. Karena kemiringan segmen ini konstan, kecepatan benda pada t = 5 adalah konstan. Karena kecepatan konstan berarti tidak ada percepatan, a = 0.

Soal 2
Kecepatan benda selama interval waktu 10 detik ditunjukkan oleh grafik di bawah ini:

(a) Tentukan jarak total objek yang dilalui dan perpindahan.
(b) Pada t = 0, posisi objek adalah x = 2 m. Temukan posisi objek pada t = 2, t = 4, t = 7, dan t = 10.
(c) Berapakah percepatan objek pada waktu-waktu berikut: t = 1, t = 3, dan t = 6.
(d) Sketsa percepatan yang sesuai dengan grafik waktu dari t = 0 hingga t = 10.

Jawab:
(a) Ingat bahwa persamaan untuk kecepatan adalah v = x/t. Jika kita menyelesaikan ini untuk x, kita mendapatkan x = vt. Perhatikan bahwa ini sama dengan luas persegi panjang yang sisi panjangnya v dan t, jadi kita dapat menentukan bahwa perpindahan adalah luas yang dilingkupi oleh grafik kecepatan vs waktu. Jadi, kita akan menemukan luas setiap bagian di bawah grafik:

Jarak total yang ditempuh oleh objek hanyalah jumlah dari semua luas ini: 3 + 6 + 4,5 + 2 + 2 = 17,5 m

Perpindahan ditentukan dengan cara yang sama, kecuali area di bawah sumbu x dianggap negatif: 3 + 6 + 4,5 – 2 – 2 = 9,5 m

Yang cukup menarik, luas yang tertutup oleh fungsi apa pun dapat diwakili oleh integral yang pasti. Sebagai contoh, jika grafik ini didefinisikan sebagai fungsi v(t), maka perpindahan akan menjadi integral dari 0 hingga 10 dari v(t) dt, dan total jarak yang ditempuh akan menjadi integral dari 0 hingga 10 dari |v(t)|dt

(b) Posisi benda pada suatu titik waktu tertentu dapat ditemukan dengan cara yang sama seperti kita menemukan perpindahan dalam bagian a, kecuali kali ini kita juga harus menambahkan nilai awal yang diberikan. Jadi:

x (2) = 2 + 3 = 5 m
x (4) = 2 + 3 + 6 = 11 m
x (7) = 2 + 3 + 6 + 4,5 = 15,5 m
x (10) = 2 + 3 + 6 + 4,5 – 2 – 2 = 11,5 m

Perhatikan bahwa ini juga dapat dilakukan dengan menambahkan integral dari 0 ke t dari v(t) dt ke nilai awal 2.

(c) Percepatan sesaat pada titik mana saja di sepanjang salah satu segmen garis grafik adalah sama dengan percepatan rata-rata di seluruh segmen garis tersebut. Rumus untuk percepatan adalah

a_rata-rata = Δv/Δt = (v₂ – v₁)/(t₂ – t₁), jadi:
a(t) = (v₂ – v₁)/(t₂ – t₁)
a (1) = (3 – 0)/(2 – 0) = 3/2 = 1,5 m/s²
a (3) = (3 – 3)/(4 – 2) = 0/2 = 0 m/s²
a (6) = (-2 – 3)/(9 – 4) = -5/5 = -1 m/s²

Demikian pula untuk hubungan antara kecepatan dan posisi, rumus untuk percepatan adalah sama dengan rumus kemiringan untuk grafik kecepatan vs. waktu. Jadi, kita dapat mengatakan bahwa kemiringan grafik setiap kecepatan vs waktu adalah percepatannya.

Perhatikan bahwa definisi ini mendefinisikan percepatan sebagai turunan dari kecepatan. Jadi, memang benar bahwa untuk setiap fungsi kecepatan v (t), turunannya adalah fungsi percepatan a (t). Juga, integrasi dapat digunakan untuk beralih dari fungsi percepatan ke fungsi posisi.
(d) Kita tahu bahwa percepatan sepanjang setiap segmen garis grafik kecepatan ini vs. waktu sama dengan kemiringan garis segmen. Kami menentukan kemiringan ini di bagian c, sehingga grafik percepatan akan terlihat seperti:

Grafik ini menggunakan garis horizontal, bukan titik untuk menunjukkan bahwa percepatan didefinisikan pada nilai tersebut pada titik mana pun sepanjang bagian itu. Lingkaran terbuka di akhir setiap segmen garis hanya menunjukkan bahwa pada nilai-nilai waktu, percepatan tidak didefinisikan pada salah satu nilai yang diwakili oleh garis horizontal. Pada titik-titik ini, percepatan tidak terdefinisi karena ia berubah secara instan dari satu nilai ke nilai berikutnya, yang tidak dapat direpresentasikan secara numerik.

Soal 3
Posisi benda selama interval waktu tertentu ditunjukkan oleh grafik di bawah ini:

(a) Di mana titik yang ditandai adalah kecepatan benda yang terbesar? Dan terkecil?
(b) Apakah percepatani benda positif atau negatif antara titik A dan B?
(c) Anggaplah kurva ini dapat dimodelkan oleh fungsi x (t) = t³ – 9,5t² + 23t – 9. Tentukan kecepatan dan percepatan benda pada t = 1, t = 3, dan t = 5.

(d) Menggunakan fungsi dari bagian c, tentukan posisi maksimum dan minimum objek dan kecepatan dalam interval dari t = 1 hingga t = 6.

Jawab:
(a) kecepatan adalah kemiringan grafik posisi vs waktu seperti ini. Dengan melihat garis-garis yang bersinggungan dengan kurva, kita dapat melihat titik mana yang memiliki kemiringan tertinggi dan terendah:

Melihat garis singgung merah, kita dapat segera menghilangkan titik B sebagai kandidat untuk kecepatan maksimum dan minimum, karena garis singgungnya horisontal dan dengan demikian memiliki kemiringan 0. Titik C adalah satu-satunya titik yang ditandai garis singgung memiliki kemiringan negatif, jadi titik C memiliki kecepatan terendah. Melihat titik A dan D, garis singgung titik A memiliki kemiringan positif yang curam sehingga titik A memiliki kecepatan tertinggi.

(b) Kita tahu bahwa percepatan adalah perubahan dalam kecepatan, jadi dengan menanyakan apakah percepatan positif atau negatif, kita bertanya apakah kecepatannya meningkat atau menurun. Karena kecepatan adalah kemiringan grafik ini, kita harus menentukan bagaimana kemiringan kurva berubah antara titik A dan B. Melihat diagram pada bagian a, kita melihat bahwa kemiringan pada titik A positif, dan kemiringan pada titik B adalah 0. Dengan demikian, kemiringan menurun dan kecepatan harus menurun. Oleh karena itu, percepatan benda negatif dalam interval ini.

(c) kecepatan adalah turunan dari posisi, dan percepatan adalah turunan dari kecepatan. Jadi, kita akan mulai dengan membedakan fungsi posisi dua kali:
x(t) = t³ – 9,5t² + 23t – 9
v(t) = 3t² – 19t + 23
a(t) = 6t – 19

Sekarang kita tahu kecepatan dan fungsi akselerasi, yang tersisa hanyalah menyambungkan nilai t ke dalam fungsi-fungsi ini dan menyederhanakan:
v (1) = 3 x 12 – 19 x 1 + 23 = 3 – 19 + 23 = 7 m/dtk
v (3) = 3 x 32 – 19 x 3 + 23 = 27 – 57 + 23 = -7 m / dtk
v (5) = 3 x 52 – 19 x 5 + 23 = 75 – 95 + 23 = 3 m / s
dan
a (1) = 6 x 1 – 19 = 6 – 19 = -13 m/s²
a (3) = 6 x 3 – 19 = 18 – 19 = -1 m/s²
a (5) = 6 x 5 – 19 = 30 – 19 = 11 m/s²

(d) Berpikir logis tentang grafik, kandidat yang mungkin untuk posisi maksimum dan minimum berada di titik akhir interval dan di titik-titik, seperti titik B, di mana kemiringan grafik adalah 0. Jadi, pertama kita mengatur kecepatan fungsi dari bagian c sama dengan 0 dan pecahkan untuk t:
v (t) = 3t² – 19t + 23 = 0
t = 1.63008 s atau t = 4.70326 s

Perhatikan bahwa ini dipecahkan menggunakan kalkulator grafik. Ujian tidak akan meminta Anda menyelesaikan kuadrat rumit ini dengan tangan, namun Anda mungkin harus menyelesaikan fungsi yang lebih sederhana dengan menggunakan rumus kuadrat. Selain itu, kita menyimpan sebanyak mungkin tempat desimal pada tahap ini untuk menjaga keakuratannya. Sekarang kita tahu semua waktu yang mungkin di mana posisi bisa maksimal atau minimum dalam interval, kita cukup berikan nilai-nilai  t ini ke x(t). Jangan lupa untuk memeriksa titik akhir:

x (t) = t³ – 9,5t² + 23t – 9
x(1) = 5,5 m
x(1.63008) = 7.58 m
x(4,70326) = -6,93 m
x(6) = 3 m

Kita melihat bahwa posisi minimum adalah -6,93 m, dan posisi maksimum 7,58 m. Menemukan kecepatan maksimum dan minimum dicapai dengan cara yang sama, kecuali kita mengatur fungsi percepatan sama dengan 0 dan pasang nilai t ke fungsi kecepatan:

a(t) = 6t – 19 = 0
6t = 19
t = 19/6 = 3.16667 s
v(t) = 3t² – 19t + 23
v(1) = 7 m/s
v(3,16667) = -7,08 m/s
v(6) = 17 m/s

Jadi kecepatan minimum adalah -7,08 m / s, dan kecepatan maksimum adalah 17 m / s.

Share :