Soal 1
Tentukan fluks magnetik yang melalui penampang ujung dari sebuah solenoida dengan panjang 20 cm, jari-jari 4 cm, memiliki 200 lilitan, dan menghasilkan arus 5 A. (ambil π² = 9,9)
Jawab:
Fluks magnetik diperoleh dengan menggunakan
Φ = BA cos θ
Dengan medan magnetik di ujung solenoida diberikan oleh
B = ½µ0IN/L
Maka
Φ = (½µ0IN/L)(πr2) cos 00
= ½ x (4π x 10-7 Tm/A)(5 A)(200)(π)(0,04 m)2/(0,2 m)
Φ = 16π2 Wb
Soal 2
Sebuah kereta api melaju ke arah utara dengan kecepatan 72 km/jam. Jika komponen vertikal kebawah medan magnetik bumi adalah 8 x 10-4 T. Tentukan besar dan arah GGL yang terinduksi pada poros gerbong sepanjang 1,5 m.
Jawab:
besar dan arah GGL yang terinduksi pada poros gerbong kereta api diberikan oleh
ε = LBv sin θ
= 1,5 m x 8 x 10-4 T x 1,5 m = 1,8 mV
Soal 3
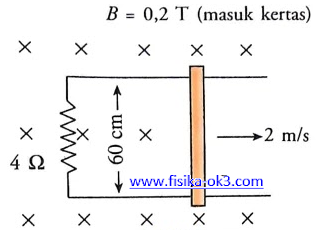
Gambar di samping menunjukkan dua keping logam besar yang diletakkan di atas rangkaian. Luas penambang rangkaian tertembus secara tegak lurus oleh medan magnet B = 0,2 T. Hambatan rangkaian adalah 4 Ω dan batang digerakkan ke kanan dengan kecepatan 2 m/s. Hitung: (a) besar dan arah arus induksi yang mengalir melalui batang logam, (b) besar dan arah gaya yang diperlukan untuk menjaga agar batang logam bergerak dengan kecepatan konstan 2 m/s dan (c) daya yang dibebaskan pada rangkaian.
Jawab:
(a) ggl induksi pada batang yaitu
ε = –LBv sin θ
(dengan θ sudut antara B dan v sama dengan 900), maka
ε = –(0,6 m)(0,2 T)(2 m/s) = –0,24 Volt
(b) arus induksi melewati logam adalah
iind = ε/R
= –0,24 Volt/4 Ω
iind = –0,06 A
dengan menggunakan aturan tangan kanan, kita peroleh arah arus induksi dalam logam mengalir dari O ke N.
(c) besar dan arah gaya yang diperlukan untuk menjaga agar batang bergerak dengan kecepatan tetap adalah
F = FL (gaya Lorentz) = iBLsin θ
(θ = 900 = sudut antara i dan B), maka
F = iBl = (–0,06 A)(0,2 T)(0,6 m) = –0,0072 N
Karena batang bergerak dengan kecepatan konstan, gaya yang diterapkan F harus menyeimbangkan gaya magnet FL pada batang saat membawa arus induksi i.
(d) daya yang dibebaskan pada rangkaian adalah
P = εiind = (–0,24 V)(–0,06 A) = 0,0144 watt
Soal 4
Sebuah kumparan dari 100 lilitan adalah tegak lurus terhadap medan magnetik sehingga fluks magnetik yang melalui kumparan adalah 300 x 10-6 Wb. Kumparan ditarik secara cepat sehingga fluks magnetik yang dilingkupinya berkurang menjadi nol dalam waktu 0,2 sekon. Tentukan ggl induksi rata rata pada kumparan.
Jawab:
ggl induksi rata rata pada kumparan diberikan oleh
ε = –N∆Φ/∆t
ε = –100 x (0 – 300 x 10-6 Wb)/0,2 s = 0,15 V
Soal 5
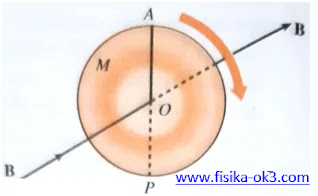
Sebuah cakram logam vertikal M dengan jari-jari 0,3 m diputar pada 5 putaran/sekon terhadap pusatnya dalam suatu medan magnetik mendatar B = 0,2 T yang berarah normal terhadap bidang acuan (lihat gambar) (a). Tentukan GGL yg diinduksikan diantara pusat O dan titik puncak A dari cakram dan (b) berapakah GGL yang diinduksikan di antara ujung-ujung diameter AP dari cakram ini?
Jawab:
(a) GGL yg diinduksikan diantara pusat O dan titik puncak A dari cakram adalah
ε = –NB∆A/∆t
ε = –NB(0 – πr2)/T
ε = NBπr2f
ε = 0,2 T x π x (0,3 m)2 x 5 = 0,09π V
(b) GGL yang diinduksikan di antara ujung-ujung diameter AP dari cakram ini adalah
ε = ½ NBπr2f
ε = ½ x 0,09π V = 0,045π V
Soal 6
Sebuah kumparan dengan jari jari 0,10 m terdiri atas 300 lilitan dan ditempatkan tegak lurus dalam suatu medan magnetik sama sebesar 0,3 tesla. Tentukan GGL induksi antara ujung-ujung kumparan jika dalam 0,2 sekon: (a) induksi magnetik menjadi nol, (b) medan magnetik dibalik arahnya dan (c) kumparan diputar 530.
Jawab:
(a) GGL induksi antara ujung-ujung kumparan jika induksi magnetik menjadi nol maka
ε = –NA cos θ(∆B/∆t)
= –300 x π x (0,10 m)2 x cos 00 x (0 – 0,3 T)/0,2 s = 4,5π V
(b) GGL induksi antara ujung-ujung kumparan jika medan magnetik dibalik arahnya maka
ε = –NAB (∆cos θ/∆t)
= –300 x π x (0,10 m)2 x 0,3 T x (cos 1800 – cos 00)/0,2 s = 9,0π V
(b) GGL induksi antara ujung-ujung kumparan jika kumparan diputar 530 maka
ε = –NBcos θ(∆A/∆t)
Dengan luas kumparan berubah dari
A1 = 0, menjadi
A2 = (530/3600)πr2, sehingga
ε = –300 x (–3070/3600)π x (0,10 m)2 x 0,3 T x cos 00)/0,2 s = 3,8375 V
Soal 7
Sebuah kumparan terdiri atas 1000 lilitan pada batang kayu berdiameter 5 cm. Kumparan tersebut memiliki hambatan 400 ohm dan dihubungkan seri dengan galvanometer yang hambatan dalamnya 225 ohm. Apabila medan magnet B = 0,0115 T yang melalui kumparan tiba-tiba ditiadakan dalam 1 detik, berapa jumlah muatan listrik yang mengalir lewat galvanometer?
Jawab:
GGL induksi pada kumparan jika induksi magnetik berubah adalah
ε = –NAcos θ (∆B/∆t)
= –1000 x π x (0,025 m)2 x cos 00 x (0 – 0,0115 T)/1 s = 7,1875π mV
Kuat arus yang melalui kumparan adalah
I = ε/(r + R) = 7,1875π x 10-3 V/(200 Ω + 425 Ω)
I = 1,15π x 10-5 A
Sehingga jumlah muatan listrik yang mengalir lewat galvanometer kita peroleh dari
n = It/qe = 1,15π x 10-5 A x 1 s/1,6 x 10-19 C = 2,258 x 1014 muatan
Tentukan fluks magnetik yang melalui penampang ujung dari sebuah solenoida dengan panjang 20 cm, jari-jari 4 cm, memiliki 200 lilitan, dan menghasilkan arus 5 A. (ambil π² = 9,9)
Jawab:
Fluks magnetik diperoleh dengan menggunakan
Φ = BA cos θ
Dengan medan magnetik di ujung solenoida diberikan oleh
B = ½µ0IN/L
Maka
Φ = (½µ0IN/L)(πr2) cos 00
= ½ x (4π x 10-7 Tm/A)(5 A)(200)(π)(0,04 m)2/(0,2 m)
Φ = 16π2 Wb
Soal 2
Sebuah kereta api melaju ke arah utara dengan kecepatan 72 km/jam. Jika komponen vertikal kebawah medan magnetik bumi adalah 8 x 10-4 T. Tentukan besar dan arah GGL yang terinduksi pada poros gerbong sepanjang 1,5 m.
Jawab:
besar dan arah GGL yang terinduksi pada poros gerbong kereta api diberikan oleh
ε = LBv sin θ
= 1,5 m x 8 x 10-4 T x 1,5 m = 1,8 mV
Soal 3
Gambar di samping menunjukkan dua keping logam besar yang diletakkan di atas rangkaian. Luas penambang rangkaian tertembus secara tegak lurus oleh medan magnet B = 0,2 T. Hambatan rangkaian adalah 4 Ω dan batang digerakkan ke kanan dengan kecepatan 2 m/s. Hitung: (a) besar dan arah arus induksi yang mengalir melalui batang logam, (b) besar dan arah gaya yang diperlukan untuk menjaga agar batang logam bergerak dengan kecepatan konstan 2 m/s dan (c) daya yang dibebaskan pada rangkaian.
Jawab:
(a) ggl induksi pada batang yaitu
ε = –LBv sin θ
(dengan θ sudut antara B dan v sama dengan 900), maka
ε = –(0,6 m)(0,2 T)(2 m/s) = –0,24 Volt
(b) arus induksi melewati logam adalah
iind = ε/R
= –0,24 Volt/4 Ω
iind = –0,06 A
dengan menggunakan aturan tangan kanan, kita peroleh arah arus induksi dalam logam mengalir dari O ke N.
(c) besar dan arah gaya yang diperlukan untuk menjaga agar batang bergerak dengan kecepatan tetap adalah
F = FL (gaya Lorentz) = iBLsin θ
(θ = 900 = sudut antara i dan B), maka
F = iBl = (–0,06 A)(0,2 T)(0,6 m) = –0,0072 N
Karena batang bergerak dengan kecepatan konstan, gaya yang diterapkan F harus menyeimbangkan gaya magnet FL pada batang saat membawa arus induksi i.
(d) daya yang dibebaskan pada rangkaian adalah
P = εiind = (–0,24 V)(–0,06 A) = 0,0144 watt
Soal 4
Sebuah kumparan dari 100 lilitan adalah tegak lurus terhadap medan magnetik sehingga fluks magnetik yang melalui kumparan adalah 300 x 10-6 Wb. Kumparan ditarik secara cepat sehingga fluks magnetik yang dilingkupinya berkurang menjadi nol dalam waktu 0,2 sekon. Tentukan ggl induksi rata rata pada kumparan.
Jawab:
ggl induksi rata rata pada kumparan diberikan oleh
ε = –N∆Φ/∆t
ε = –100 x (0 – 300 x 10-6 Wb)/0,2 s = 0,15 V
Soal 5
Sebuah cakram logam vertikal M dengan jari-jari 0,3 m diputar pada 5 putaran/sekon terhadap pusatnya dalam suatu medan magnetik mendatar B = 0,2 T yang berarah normal terhadap bidang acuan (lihat gambar) (a). Tentukan GGL yg diinduksikan diantara pusat O dan titik puncak A dari cakram dan (b) berapakah GGL yang diinduksikan di antara ujung-ujung diameter AP dari cakram ini?
Jawab:
(a) GGL yg diinduksikan diantara pusat O dan titik puncak A dari cakram adalah
ε = –NB∆A/∆t
ε = –NB(0 – πr2)/T
ε = NBπr2f
ε = 0,2 T x π x (0,3 m)2 x 5 = 0,09π V
(b) GGL yang diinduksikan di antara ujung-ujung diameter AP dari cakram ini adalah
ε = ½ NBπr2f
ε = ½ x 0,09π V = 0,045π V
Soal 6
Sebuah kumparan dengan jari jari 0,10 m terdiri atas 300 lilitan dan ditempatkan tegak lurus dalam suatu medan magnetik sama sebesar 0,3 tesla. Tentukan GGL induksi antara ujung-ujung kumparan jika dalam 0,2 sekon: (a) induksi magnetik menjadi nol, (b) medan magnetik dibalik arahnya dan (c) kumparan diputar 530.
Jawab:
(a) GGL induksi antara ujung-ujung kumparan jika induksi magnetik menjadi nol maka
ε = –NA cos θ(∆B/∆t)
= –300 x π x (0,10 m)2 x cos 00 x (0 – 0,3 T)/0,2 s = 4,5π V
(b) GGL induksi antara ujung-ujung kumparan jika medan magnetik dibalik arahnya maka
ε = –NAB (∆cos θ/∆t)
= –300 x π x (0,10 m)2 x 0,3 T x (cos 1800 – cos 00)/0,2 s = 9,0π V
(b) GGL induksi antara ujung-ujung kumparan jika kumparan diputar 530 maka
ε = –NBcos θ(∆A/∆t)
Dengan luas kumparan berubah dari
A1 = 0, menjadi
A2 = (530/3600)πr2, sehingga
ε = –300 x (–3070/3600)π x (0,10 m)2 x 0,3 T x cos 00)/0,2 s = 3,8375 V
Soal 7
Sebuah kumparan terdiri atas 1000 lilitan pada batang kayu berdiameter 5 cm. Kumparan tersebut memiliki hambatan 400 ohm dan dihubungkan seri dengan galvanometer yang hambatan dalamnya 225 ohm. Apabila medan magnet B = 0,0115 T yang melalui kumparan tiba-tiba ditiadakan dalam 1 detik, berapa jumlah muatan listrik yang mengalir lewat galvanometer?
Jawab:
GGL induksi pada kumparan jika induksi magnetik berubah adalah
ε = –NAcos θ (∆B/∆t)
= –1000 x π x (0,025 m)2 x cos 00 x (0 – 0,0115 T)/1 s = 7,1875π mV
Kuat arus yang melalui kumparan adalah
I = ε/(r + R) = 7,1875π x 10-3 V/(200 Ω + 425 Ω)
I = 1,15π x 10-5 A
Sehingga jumlah muatan listrik yang mengalir lewat galvanometer kita peroleh dari
n = It/qe = 1,15π x 10-5 A x 1 s/1,6 x 10-19 C = 2,258 x 1014 muatan

Post a Comment for "Soal Induksi Elektromagnetik dan pembahasannya 5"
Sobat Fisika! Berikan Komentar di kolom komentar dengan bahasa yang sopan dan sesuai isi konten...Terimasih untuk kunjunganmu di blog ini, semoga bermanfaat!