Soal 1
Posisi sebuah benda dinyatakan dengan persamaan: r = {7ti + (9t + 3t²)j} m. Setelah benda bergerak selama 2,5 sekon, kelajuannya menjadi. . . .
A. 15 m/s
B. 20 m/s
C. 25 m/s
D. 30 m/s
E. 35 m/s
Jawab: C
Kecepatan benda dinyatakan sebagai
v = dr/dt = d{7ti + (9t + 3t²)j}/dt
v = 7i + (9 + 6t)j
saat t = 2,5 s,
v = 7i + (9 + 6 x 2,5)j = 7i + 24j
kelajuan merupakan besar dari kecepatan, maka
v = √[vx2 + vy2]
v = √[(7)2 + (24)2] = 25 m/s
Soal 2
Gerak sebuah benda memiliki persamaan posisi :
r = (8t - 4)i + (-3t2 + 6t)j
Semua besaran menggunakan satuan dasar SI.
(1) Benda bergerak berubah beraturan
(2) Memiliki koordinat awal (-4,0) m
(3) Setelah 1 s , perpindahannya 5 m
(4) Setelah 1 s , kecepatannya menjadi 8 m/s
Pernyataan yang berkaitan dengan gerak benda adalah . . . .
A. (1) dan (3)
B. (1) dan (4)
C. (2) dan (4)
D. (1), (2) dan (3)
E. (2), (3), dan (4)
Jawab: E
koordinat, r (x , y) = (– 4, 0) m
besarnya perpindahan adalah
r = √(x2 + y2) = √(42 + 32) = 5 m
v = 8i + (-6t + 6)j
saat t = 1 s,
v = 8i m/s
besar kecepatan 8 m/s
a = –6j
percepatan benda tidak bergantung waktu artinya benda bergerak dengan dengan percepatan konstan pada sumbu y tapi sekaligus bergerak dengan kecepatan tetap pada sumbu x (gerak parabola)
Soal 3
Sebuah partikel bergerak lurus dengan persamaan kecepatan v = [5i + (2t - 1/3)j] m/s. Jika posisi partikel mula-mula di pusat koordinat, maka perpindahan partikel selama 3 sekon adalah . . . .
A. 13 m
B. 14 m
C. 15 m
D. 16 m
E. 17 m
Jawab:
Posisi partikel dinyatakan oleh
r = r0 + ∫vdt
r = 0 + ∫[5i + (2t - 1/3)j]dt
r = [5ti + (t2 – t/3)j] m
saat t = 3,0 s
r (t = 3,0 s) = [5 x 3 i + (32 – 3/3)j] m
r (t = 3,0 s) = (15i + 8j) m
besarnya perpindahan adalah
r = √(x2 + y2) = √(152 + 82) = 17 m
Soal 4
Sebuah sungai mengalir dari barat ke timur pada kelajuan 5 m/menit. Seorang anak di tepi selatan sungai mampu berenang dengan kelajuan 10 m/menit dalam air tenang. Jika anak itu ingin berenang menyeberangi sungai dengan lintasan terpendek, ia harus berenang dengan sudut θ terhadap arah utara. Nilai sin θ adalah . . . .
A. √5/5
B. ½
C. 2√3/3
D. 2
E. 3√2/2
Jawab:
Dari gambar terlihat bahwa Jika anak itu ingin berenang menyeberangi sungai dengan lintasan terpendek (lintasan AB), ia harus berenang dengan sudut θ terhadap arah utara (ke titik C). Agar ini dapat terjadi, maka va sin θ harus sama dengan vs (kecepatan sungai).
va sin θ = vs
sin θ = vs/va = (5 m/menit)/(10 m/menit)
sin θ = ½
Soal 5
Air sungai mengalir dari barat ke timur pada kelajuan c. Seorang anak berenang searah arus sungai dengan kelajuan v sampai menempuh jarak d. Kemudian anak tersebut berbalik arah dan berenang menuju titik berangkatnya semula. Selang waktu yang ditempuh anak itu adalah . . . .
A. 2d/(v + c)
B. 2d/(v – c)
C. 3dv/(v2 + c2)
D. 2dv/(v2 – c2)
E. 2dv/(v2 + c2)
Jawab: D
Jarak yang ditempuh d. Anak bergerak dari P ke Q dengan kecepatan v + c (kecepatan anak + kecepatan arus) dan dari Q ke P dengan kecepatan: v − c. Jadi waktu yang diperlukan oleh anak adalah:
t = d/(v + c) + d/(v - c)
t = 2dv/(v2 – c2)
Soal 6
Sebuah pesawat menempuh suatu jalur lurus dari A ke B dan berbalik lagi. Jarak antara A dan B adalah L dan pesawat bergerak dengan kelajuan tetap v terhadap udara. Saat itu ada angin bertiup dengan kelajuan tetap u. Jika angin bertiup tegak lurus terhadap garis AB maka waktu total perjalanan pesawat adalah . . . .
A. 2Lv/(v2 – u2)
B. 2Lv/√(v2 + u2)
C. 2L/(v – u)
D. 2L/√(v2 – u2)
E. 2L/√(v2 + u2)
Jawab: D
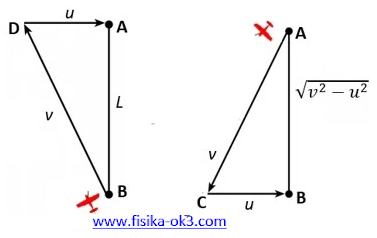
Untuk mencapai titik C, pesawat harus diarahkan ketitik C (lihat gambar). Jadi kecepatan arah AB adalah:
vAB = √(v2 – u2)
Untuk balik dari B ke A pesawat harus diarahkan ke arah D. Kecepatan arah BA adalah:
vBA = √(v2 – u2)
Jadi waktu yang diperlukan oleh pesawat pada lintasan ABA adalah:
T = 2L/√(v2 – u2)
Soal 7
Sebuah peluru menempuh lintasan parabola di dekat permukaan bumi. Pernyataan yang benar tentang besar gaya resultan, arah gaya resultan, dan sudut antara gaya resultan terhadap arah lintasan adalah . . . .
Jawab: A
Gaya resultan pada peluruh adalah gaya gravitasi.
Posisi sebuah benda dinyatakan dengan persamaan: r = {7ti + (9t + 3t²)j} m. Setelah benda bergerak selama 2,5 sekon, kelajuannya menjadi. . . .
A. 15 m/s
B. 20 m/s
C. 25 m/s
D. 30 m/s
E. 35 m/s
Jawab: C
Kecepatan benda dinyatakan sebagai
v = dr/dt = d{7ti + (9t + 3t²)j}/dt
v = 7i + (9 + 6t)j
saat t = 2,5 s,
v = 7i + (9 + 6 x 2,5)j = 7i + 24j
kelajuan merupakan besar dari kecepatan, maka
v = √[vx2 + vy2]
v = √[(7)2 + (24)2] = 25 m/s
Soal 2
Gerak sebuah benda memiliki persamaan posisi :
r = (8t - 4)i + (-3t2 + 6t)j
Semua besaran menggunakan satuan dasar SI.
(1) Benda bergerak berubah beraturan
(2) Memiliki koordinat awal (-4,0) m
(3) Setelah 1 s , perpindahannya 5 m
(4) Setelah 1 s , kecepatannya menjadi 8 m/s
Pernyataan yang berkaitan dengan gerak benda adalah . . . .
A. (1) dan (3)
B. (1) dan (4)
C. (2) dan (4)
D. (1), (2) dan (3)
E. (2), (3), dan (4)
Jawab: E
- Koordinat awal, t = 0, maka
koordinat, r (x , y) = (– 4, 0) m
- Perpindahan setelah t = 1 s,
besarnya perpindahan adalah
r = √(x2 + y2) = √(42 + 32) = 5 m
- Kecepatan benda dinyatakan sebagai
v = 8i + (-6t + 6)j
saat t = 1 s,
v = 8i m/s
besar kecepatan 8 m/s
- Percepatan benda dinyatakan sebagai
a = –6j
percepatan benda tidak bergantung waktu artinya benda bergerak dengan dengan percepatan konstan pada sumbu y tapi sekaligus bergerak dengan kecepatan tetap pada sumbu x (gerak parabola)
Soal 3
Sebuah partikel bergerak lurus dengan persamaan kecepatan v = [5i + (2t - 1/3)j] m/s. Jika posisi partikel mula-mula di pusat koordinat, maka perpindahan partikel selama 3 sekon adalah . . . .
A. 13 m
B. 14 m
C. 15 m
D. 16 m
E. 17 m
Jawab:
Posisi partikel dinyatakan oleh
r = r0 + ∫vdt
r = 0 + ∫[5i + (2t - 1/3)j]dt
r = [5ti + (t2 – t/3)j] m
saat t = 3,0 s
r (t = 3,0 s) = [5 x 3 i + (32 – 3/3)j] m
r (t = 3,0 s) = (15i + 8j) m
besarnya perpindahan adalah
r = √(x2 + y2) = √(152 + 82) = 17 m
Soal 4
Sebuah sungai mengalir dari barat ke timur pada kelajuan 5 m/menit. Seorang anak di tepi selatan sungai mampu berenang dengan kelajuan 10 m/menit dalam air tenang. Jika anak itu ingin berenang menyeberangi sungai dengan lintasan terpendek, ia harus berenang dengan sudut θ terhadap arah utara. Nilai sin θ adalah . . . .
A. √5/5
B. ½
C. 2√3/3
D. 2
E. 3√2/2
Jawab:
Dari gambar terlihat bahwa Jika anak itu ingin berenang menyeberangi sungai dengan lintasan terpendek (lintasan AB), ia harus berenang dengan sudut θ terhadap arah utara (ke titik C). Agar ini dapat terjadi, maka va sin θ harus sama dengan vs (kecepatan sungai).
va sin θ = vs
sin θ = vs/va = (5 m/menit)/(10 m/menit)
sin θ = ½
Soal 5
Air sungai mengalir dari barat ke timur pada kelajuan c. Seorang anak berenang searah arus sungai dengan kelajuan v sampai menempuh jarak d. Kemudian anak tersebut berbalik arah dan berenang menuju titik berangkatnya semula. Selang waktu yang ditempuh anak itu adalah . . . .
A. 2d/(v + c)
B. 2d/(v – c)
C. 3dv/(v2 + c2)
D. 2dv/(v2 – c2)
E. 2dv/(v2 + c2)
Jawab: D
Jarak yang ditempuh d. Anak bergerak dari P ke Q dengan kecepatan v + c (kecepatan anak + kecepatan arus) dan dari Q ke P dengan kecepatan: v − c. Jadi waktu yang diperlukan oleh anak adalah:
t = d/(v + c) + d/(v - c)
t = 2dv/(v2 – c2)
Soal 6
Sebuah pesawat menempuh suatu jalur lurus dari A ke B dan berbalik lagi. Jarak antara A dan B adalah L dan pesawat bergerak dengan kelajuan tetap v terhadap udara. Saat itu ada angin bertiup dengan kelajuan tetap u. Jika angin bertiup tegak lurus terhadap garis AB maka waktu total perjalanan pesawat adalah . . . .
A. 2Lv/(v2 – u2)
B. 2Lv/√(v2 + u2)
C. 2L/(v – u)
D. 2L/√(v2 – u2)
E. 2L/√(v2 + u2)
Jawab: D
Untuk mencapai titik C, pesawat harus diarahkan ketitik C (lihat gambar). Jadi kecepatan arah AB adalah:
vAB = √(v2 – u2)
Untuk balik dari B ke A pesawat harus diarahkan ke arah D. Kecepatan arah BA adalah:
vBA = √(v2 – u2)
Jadi waktu yang diperlukan oleh pesawat pada lintasan ABA adalah:
T = 2L/√(v2 – u2)
Soal 7
Sebuah peluru menempuh lintasan parabola di dekat permukaan bumi. Pernyataan yang benar tentang besar gaya resultan, arah gaya resultan, dan sudut antara gaya resultan terhadap arah lintasan adalah . . . .
| Besar gaya resultan | Arah gaya resultan | Susut antara gaya resultan terhadap lintasan | |
| A | Konstan | Konstan | Konstan |
| B | Konstan | Konstan | Berubah |
| C | Konstan | Berubah | Konstan |
| D | Berubah | Konstan | Konstan |
| E | Berubah | Berubah | Konstan |
Jawab: A
Gaya resultan pada peluruh adalah gaya gravitasi.


Post a Comment for "Soal Gerak Dua Dimensi dan Pembahasannya"
Sobat Fisika! Berikan Komentar di kolom komentar dengan bahasa yang sopan dan sesuai isi konten...Terimasih untuk kunjunganmu di blog ini, semoga bermanfaat!