Soal 1
Sebuah paket logistik dijatuhkan dari sebuah pesawat tanpa kecepatan awal relatif terhadap pesawat. Saat menjatuhkan paket, pesawat tersebut berada pada ketinggian h dan sedang bergerak dengan kecepatan u dalam arah horizontal. Agar bom mendarat tepat pada sasaran, jarak horizontal pesawat dari target pendaratan saat pilot menjatuhkan paket adalah . . . .
A. u√(h/g)
B. u√(h/2g)
C. u√(2h/g)
D. 2u√(h/g)
E. 2u√(2h/g)
Jawab: C
Paket akan jatuh dengan lintasan parabola seperti gambar di bawah ini.
Dengan v0x = u, v0y = 0, paket tiba pada sasaran y = 0, dan y0 = h, maka dengan menggunakan
y = y0 + v0yt – ½ gt2
0 = h + 0 – ½ gt2
Maka
t = √(2h/g) (waktu paket sampai di sasaran)
sehingga jarak horisontalnya adalah
d = v0xt
d = u√(2h/g)
Soal 2
Sebuah bola dilempar horizontal dari puncak sebuah menara yang tingginya h meter. Bola menumbuk tanah pada sebuah titik sejauh x meter dari kaki menara. Jika gravitasi adalah g dan sudut yang dibentuk oleh vektor kecepatan terhadap arah horizontal tepat sesaat sebelum bola menumbuk tanah adalah θ. Maka tan θ adalah . . . .
A. √(2h/x)
B. √(h/2x)
C. 2x/h
D. h/2x
E. 2h/x
Jawab:
Dengan, v0x, v0y = 0, bola tiba di tanah y = 0, dan y0 = h, maka dengan menggunakan
y = y0 + v0yt – ½ gt2
0 = h + 0 – ½ gt2
Maka
t = √(2h/g) (waktu bola sampai di sasaran)
sehingga kecepatan horisontalnya adalah
v0x = x/t = x/√(2h/g)
kecepatan vertikal ketika bola sampai tanah
vy = v0y – gt = 0 - g√(2h/g)
Maka tan θ adalah
tan θ = vy/v0x
tan θ = - g√(2h/g)/[x/√(2h/g)]
tan θ = -2h/x or tan θ = 2h/x
Soal 3
Gambar dibawah menunjukkan sebuah bola yang ditendang dari sebuah pamggung yang tingginya 1,2 m pada kelajuan awal 10,0 m/s dan sudut elevasi θ = 30° terhadap horizontal.
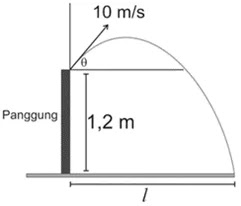
Jarak mendatar L yang ditempuh bola ketika bola itu mengenai tanah adalah . . . .
A. 6,8 m
B. 7,5 m
C. 9,0 m
D. 10,2 m
E. 11,4 m
Jawab: D
Kecepatan awal sumbu x,
v0x = v0 cos θ = 10,0 m/s cos 300 = 5√3 m/s
Kecepatan awal sumbu y,
v0y = v0 sin θ = 10,0 m/s sin 300 = 5 m/s,
Bola tiba di tanah y = 0 (acuan), dan y0 = 1,2 m, maka dengan menggunakan
y = y0 + v0yt – ½ gt)) = 1,2 + 5t – ½(10)t2
t2 – t – 0,24 = 0
(t – 1,2)(t + 0,2) = 0
Maka waktu bola mencapai tanah t = 1,2 s
Jadi, jarak horisontal l = v0xt = 5√3 m/s x 1,2 s = 10,4 m
Sebuah paket logistik dijatuhkan dari sebuah pesawat tanpa kecepatan awal relatif terhadap pesawat. Saat menjatuhkan paket, pesawat tersebut berada pada ketinggian h dan sedang bergerak dengan kecepatan u dalam arah horizontal. Agar bom mendarat tepat pada sasaran, jarak horizontal pesawat dari target pendaratan saat pilot menjatuhkan paket adalah . . . .
A. u√(h/g)
B. u√(h/2g)
C. u√(2h/g)
D. 2u√(h/g)
E. 2u√(2h/g)
Jawab: C
Paket akan jatuh dengan lintasan parabola seperti gambar di bawah ini.
Dengan v0x = u, v0y = 0, paket tiba pada sasaran y = 0, dan y0 = h, maka dengan menggunakan
y = y0 + v0yt – ½ gt2
0 = h + 0 – ½ gt2
Maka
t = √(2h/g) (waktu paket sampai di sasaran)
sehingga jarak horisontalnya adalah
d = v0xt
d = u√(2h/g)
Soal 2
Sebuah bola dilempar horizontal dari puncak sebuah menara yang tingginya h meter. Bola menumbuk tanah pada sebuah titik sejauh x meter dari kaki menara. Jika gravitasi adalah g dan sudut yang dibentuk oleh vektor kecepatan terhadap arah horizontal tepat sesaat sebelum bola menumbuk tanah adalah θ. Maka tan θ adalah . . . .
A. √(2h/x)
B. √(h/2x)
C. 2x/h
D. h/2x
E. 2h/x
Jawab:
Dengan, v0x, v0y = 0, bola tiba di tanah y = 0, dan y0 = h, maka dengan menggunakan
y = y0 + v0yt – ½ gt2
0 = h + 0 – ½ gt2
Maka
t = √(2h/g) (waktu bola sampai di sasaran)
sehingga kecepatan horisontalnya adalah
v0x = x/t = x/√(2h/g)
kecepatan vertikal ketika bola sampai tanah
vy = v0y – gt = 0 - g√(2h/g)
Maka tan θ adalah
tan θ = vy/v0x
tan θ = - g√(2h/g)/[x/√(2h/g)]
tan θ = -2h/x or tan θ = 2h/x
Soal 3
Gambar dibawah menunjukkan sebuah bola yang ditendang dari sebuah pamggung yang tingginya 1,2 m pada kelajuan awal 10,0 m/s dan sudut elevasi θ = 30° terhadap horizontal.

Jarak mendatar L yang ditempuh bola ketika bola itu mengenai tanah adalah . . . .
A. 6,8 m
B. 7,5 m
C. 9,0 m
D. 10,2 m
E. 11,4 m
Jawab: D
Kecepatan awal sumbu x,
v0x = v0 cos θ = 10,0 m/s cos 300 = 5√3 m/s
Kecepatan awal sumbu y,
v0y = v0 sin θ = 10,0 m/s sin 300 = 5 m/s,
Bola tiba di tanah y = 0 (acuan), dan y0 = 1,2 m, maka dengan menggunakan
y = y0 + v0yt – ½ gt)) = 1,2 + 5t – ½(10)t2
t2 – t – 0,24 = 0
(t – 1,2)(t + 0,2) = 0
Maka waktu bola mencapai tanah t = 1,2 s
Jadi, jarak horisontal l = v0xt = 5√3 m/s x 1,2 s = 10,4 m


Post a Comment for "Soal Gerak Parabola dan Pembahasannya 1"
Sobat Fisika! Berikan Komentar di kolom komentar dengan bahasa yang sopan dan sesuai isi konten...Terimasih untuk kunjunganmu di blog ini, semoga bermanfaat!