Soal 1
Dua bola masing masing bermassa 6kg dan 4kg dengan jarak antara pusatnya adalah 2m di tunjukkan seperti gambar di samping. Tentukan gaya gravitasi di antara kedua bola tersebut.
Jawab:
Gaya gravitasi antara dua benda yang bermassa m1 dan m2 pada jarak r12 dinyatakan sebagai
F12 = Gm1m2/r122
Dengan G = konstanta gravitasi = 6,67 x 10-11 Nm2/kg2, Maka
F12 = (6,67 x 10-11 Nm2/kg2)(6 kg)(4 kg)/(2 m)2 = 4,0 x 10-10 N
Soal 2
Explorer 38 adalah sebuah satelit peneliti radio astronomi yang bermassa a kg, mengitari bumi dalam suatu orbit yang berjari-jari 3R/2 dimana R adalah jari-jari Bumi. Anggap gaya gravitasi pada massa 1 kg di permukaan bumi 10 N. Hitunglah gaya gravitasi pada satelit itu.
Jawab:
Percepatan gravitasi pada orbit satelit dinyatakan sebagai
g' = GM/r2
dengan M = massa Bumi dan r = jarak satelit dari pusat Bumi
maka ketika satelit berada pada posisi 3R/2 dari pusat Bumi, percepatan gravitasi yang dialami adalah
g’ = GM/(3R/2)2 = (4/9) GM/R2 = 4g/9
dengan g = GM/R2 adalah percepatan gravitasi ketika benda berada di dekat permukaan Bumi, sehingga
g’ = 4(10 N/kg)/9 = 40/9 m/s2
jadi, gaya gravitasi pada satelit tersebut adalah
F = msatelitg’ = 40a/9 N
Soal 3
Dua buah partikel bermassa 0.20 kg dan 0,30 kg terpisah sejauh 0,15 m. Partikel ketiga yang bermassa 0,050 kg diletakkan diantara keduanya dan pada garis hubung kedua partikel itu.
(a) Hitung gaya gravitasi yang bekerja pada partikel ketiga jika partikel itu diletakkan 0,005 m dari benda bermassa 0.30 kg.
(b) Dimanakah di antara garis hubung tersebut partikel ketiga harus diletakkan agar gravitasi tidak bekerja pada partikel itu?
Jawab:
(a) gaya-gaya yang bekerjapada partikel ketiga ditunjukkan pada gambar di bawah ini,
Pada benda tiga bekerja gaya F13 dan F32 yang masing-masing besarnya adalah
F31 = Gm1m3/r132 = G(0,20 kg)(0,050 kg)/(0,10 m)2 = G N
F32 = Gm2m3/r232 = G(0,30 kg)(0,050 kg)/(0,050 m)2 = 6G N
Maka total gaya yang bekerja pada massa tiga adalah
∑F3 = F31 + F32
∑F3 = –G + (6G)
∑F3 = 5G = 5(6,67 x 10-11 Nm2/kg2) = 3,335 x 10-10 N
(b) Misalkan benda tiga diletakkan x meter dari benda satu, maka posisi benda tiga berada pada (0,15 – x) m dari benda satu.
Agar gaya gravitasi tidak bekerja pada benda tiga maka berlaku
∑F3 = F31 + F32 = 0
F31 = F32
Gm1m3/r132 = Gm2m3/r232
0,20/x2 = 0,30/(0,15 – x)2
0,45/x = 0,55/(0,15 – x)
0,55x = 0,0675 – 0,45x
x = 0,0675 m
benda tiga harus diletakkan sekitar 0,0675 m dari benda satu agar benda tiga tidak merasakan gaya tarik akibat kedua benda.
Soal 4
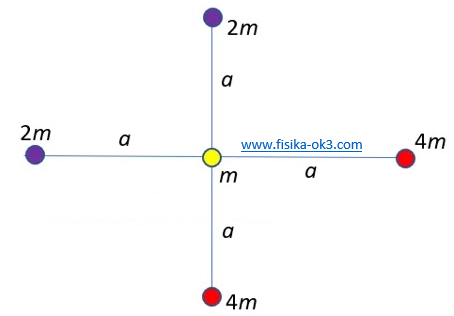
Hitung besar dan arah resultan gaya gravitasi yang bekerja pada benda bermassa m (lihat gambar di samping). Nyatakan jawaban anda dalam G, m dan a.
Jawab:
Gaya interaksi antara m dan 2m adalah
F1 = G(m)(2m)/a2 = 2Gm2/a2 = F
Gaya interaksi antara m dan 4m adalah
F2 = G(m)(4m)/a2 = 4Gm2/a2 = 2F
Maka resultan gaya yang bekerja pada benda m dan 2m adalah
∑F1 = √[F2 + F2]= F√2 atau
Maka resultan gaya yang bekerja pada benda m dan 4m adalah
∑F2 = √[(2F)2 + (2F)2]= 2F√2 atau
Dari gambar di atas ∑F1 dan ∑F2 masing-masing membentuk sudut 450 terhadap sumbu x, maka ∑F1 dan ∑F2 sejajar, maka total gaya yang bekerja pada benda m adalah
∑F = F1 + F2
∑F = 2F√2 – F√2 = F√2
∑F = 2√2Gm2/a2
Dan arah ∑F = –450 terhadap sumbu x atau 3150 terhadap sumbu x.
Dua bola masing masing bermassa 6kg dan 4kg dengan jarak antara pusatnya adalah 2m di tunjukkan seperti gambar di samping. Tentukan gaya gravitasi di antara kedua bola tersebut.
Jawab:
Gaya gravitasi antara dua benda yang bermassa m1 dan m2 pada jarak r12 dinyatakan sebagai
F12 = Gm1m2/r122
Dengan G = konstanta gravitasi = 6,67 x 10-11 Nm2/kg2, Maka
F12 = (6,67 x 10-11 Nm2/kg2)(6 kg)(4 kg)/(2 m)2 = 4,0 x 10-10 N
Soal 2
Explorer 38 adalah sebuah satelit peneliti radio astronomi yang bermassa a kg, mengitari bumi dalam suatu orbit yang berjari-jari 3R/2 dimana R adalah jari-jari Bumi. Anggap gaya gravitasi pada massa 1 kg di permukaan bumi 10 N. Hitunglah gaya gravitasi pada satelit itu.
Jawab:
Percepatan gravitasi pada orbit satelit dinyatakan sebagai
g' = GM/r2
dengan M = massa Bumi dan r = jarak satelit dari pusat Bumi
maka ketika satelit berada pada posisi 3R/2 dari pusat Bumi, percepatan gravitasi yang dialami adalah
g’ = GM/(3R/2)2 = (4/9) GM/R2 = 4g/9
dengan g = GM/R2 adalah percepatan gravitasi ketika benda berada di dekat permukaan Bumi, sehingga
g’ = 4(10 N/kg)/9 = 40/9 m/s2
jadi, gaya gravitasi pada satelit tersebut adalah
F = msatelitg’ = 40a/9 N
Soal 3
Dua buah partikel bermassa 0.20 kg dan 0,30 kg terpisah sejauh 0,15 m. Partikel ketiga yang bermassa 0,050 kg diletakkan diantara keduanya dan pada garis hubung kedua partikel itu.
(a) Hitung gaya gravitasi yang bekerja pada partikel ketiga jika partikel itu diletakkan 0,005 m dari benda bermassa 0.30 kg.
(b) Dimanakah di antara garis hubung tersebut partikel ketiga harus diletakkan agar gravitasi tidak bekerja pada partikel itu?
Jawab:
(a) gaya-gaya yang bekerjapada partikel ketiga ditunjukkan pada gambar di bawah ini,
Pada benda tiga bekerja gaya F13 dan F32 yang masing-masing besarnya adalah
F31 = Gm1m3/r132 = G(0,20 kg)(0,050 kg)/(0,10 m)2 = G N
F32 = Gm2m3/r232 = G(0,30 kg)(0,050 kg)/(0,050 m)2 = 6G N
Maka total gaya yang bekerja pada massa tiga adalah
∑F3 = F31 + F32
∑F3 = –G + (6G)
∑F3 = 5G = 5(6,67 x 10-11 Nm2/kg2) = 3,335 x 10-10 N
(b) Misalkan benda tiga diletakkan x meter dari benda satu, maka posisi benda tiga berada pada (0,15 – x) m dari benda satu.
Agar gaya gravitasi tidak bekerja pada benda tiga maka berlaku
∑F3 = F31 + F32 = 0
F31 = F32
Gm1m3/r132 = Gm2m3/r232
0,20/x2 = 0,30/(0,15 – x)2
0,45/x = 0,55/(0,15 – x)
0,55x = 0,0675 – 0,45x
x = 0,0675 m
benda tiga harus diletakkan sekitar 0,0675 m dari benda satu agar benda tiga tidak merasakan gaya tarik akibat kedua benda.
Soal 4
Hitung besar dan arah resultan gaya gravitasi yang bekerja pada benda bermassa m (lihat gambar di samping). Nyatakan jawaban anda dalam G, m dan a.
Jawab:
Gaya interaksi antara m dan 2m adalah
F1 = G(m)(2m)/a2 = 2Gm2/a2 = F
Gaya interaksi antara m dan 4m adalah
F2 = G(m)(4m)/a2 = 4Gm2/a2 = 2F
Maka resultan gaya yang bekerja pada benda m dan 2m adalah
∑F1 = √[F2 + F2]= F√2 atau
Maka resultan gaya yang bekerja pada benda m dan 4m adalah
∑F2 = √[(2F)2 + (2F)2]= 2F√2 atau
Dari gambar di atas ∑F1 dan ∑F2 masing-masing membentuk sudut 450 terhadap sumbu x, maka ∑F1 dan ∑F2 sejajar, maka total gaya yang bekerja pada benda m adalah
∑F = F1 + F2
∑F = 2F√2 – F√2 = F√2
∑F = 2√2Gm2/a2
Dan arah ∑F = –450 terhadap sumbu x atau 3150 terhadap sumbu x.




Post a Comment for "Soal dan Pembahasan Hukum Newton tentang Gravitasi 4"
Sobat Fisika! Berikan Komentar di kolom komentar dengan bahasa yang sopan dan sesuai isi konten...Terimasih untuk kunjunganmu di blog ini, semoga bermanfaat!