Soal dan Pembahasan Hukum Newton tentang Gravitasi

Soal 1
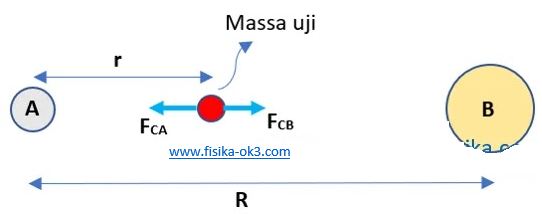
Massa planet A sekitar 4 kali massa planet B dan jarak antarpusat planet A ke planet B adalah R. Suatu benda uji bermassa M yang berada pada jarak r dari pusat planet A dan pada garis lurus yang menghubungkan kedua planet memiliki gaya gravitasi nol. Jarak r tersebut adalah . . . .R.
A. 0,25
B. 0,5
C. 2/3
D. 0,75
E. 0,8

Jawab: C


Jika tidak ada pengaruh gravitasi pada massa uji akibat kedua planet, maka pada massa uji berlaku
∑F = 0

F­_CB – F_CA = 0

kMm­_A/r² = kMm_B/(R – r)²

4m_B/r² = m_B/(R – r)²

2/r = 1/(R – r)

r = 2R – 2r

r = 2R/3

Soal 2
Perhatikan gambar satelit berikut.


Satelit bermassa sangat besar dan berongga dengan seluruh massanya berlokasi pada jari-jari R dari pusatnya. Grafik terbaik yang menampilkan gaya gravitasi yang dialami oleh seorang astronot pada jarak r dari pusat satelit dengan r mulai dari 0 sampai ~ adalah . . . .

Jawab:
Misalkan massa rongga berjari-jari R adalah m₀ dan volumenya V₀ = 4πR³/3.

Volume benda M berjari-jari r adalah V = 4πr³/3,

Hubungan massa m₀ dan M adalah

m₀/(4πR³/3) = M/(4πr³/3)

m₀ = MR³/r³

Gaya gravitasi yang terjadi adalah (m massa uji)

F = GmM/R²

F = G(MR³/r³)m/R²

F = [GmM/r³]R

Gaya F sebanding dengan R,

F_maks = GmM/R² (ketika r = R)

Jadi grafik yang benar untuk kasus ini adalah

Di luar satelit, gaya gravitasinya bekerja pada astronot sebagai hukum kuadrat terbalik, seolah-olah massa berada di pusat massa. Di dalam satelit, efek gravitasi dari distribusi massa bertambah hingga menghasilkan gaya gravitasi bersih 0 pada astronot.
Grafik terbaik yang menampilkan gaya gravitasi yang dialami oleh seorang astronot pada jarak r dari pusat satelit dengan r mulai dari 0 sampai ~ adalah



Soal 3
Dua buah planet berbentuk bola mempunyai rapat massa rata-rata sama, sedangkan jari-jarinya R₁ dan R₂. Perbandingan medan gravitasi pada permukaan planet pertama terhadap medan gravitasi pada permukaan planet kedua adalah . . . .
A. R₁ : R₂
B. R₂ : R₁
C. R₁² : R₂²
D. R₂² : R₁²
E. √R₁ : √R₂

Jawab:
Medan gravitasi planet 1 dan 2 diberikan oleh

g₁ = GM₁/R₁² dan g₂ = GM₂/R₂²

kita cari dahulu hubungan kedua massa planet. Karena massa jenis kedua planet sama maka,
M₁/(4πR₁³/3) = M₂/(4πR₂³/3)

M₁/M₂ = (R₁/R₂)³

Perbandingan medan gravitasi kedua planet adalah

g₁/g₂ = (M₁/M₂)(R₂/R₁)²

g₁/g₂ = (R₁/R₂)³(R₂/R₁)² = R₁ : R₂

Soal 4
Sebuah bintang yang baru terbentuk memiliki kerapatan ρ, jari-jari R dan percepatan gravitasi pada permukaan sebesar g. Dalam perkembangannya, bintang tersebut mengembang hingga memiliki kerapatan ρ₁ = 0,75ρ dan jari-jari R₁ = 1,25 R. Percepatan gravitasi di permukaannya pada keadaan standar tersebut adalah . . . .
A. 9g/25
B. 18g/25
C. 9g/16
D. 15g/16
E. g

Jawab:
Percepatan gravitasi sebuah bintang dinyatakan oleh

g = GM/r²

massa jenis bintang adalah

ρ = M/(4πr³/3) = 3M/4πr³

aka jika dinyakatan dalam massa jenis, percepatan gravitasi bintang adalah

g = 4πGρr/3

Untuk bintang yang memiliki jari-jari R dan massa jenis ρ, percepatan gravitasinya adalah

g = 4πGρR/3

Bintang tersebut mengembang hingga memiliki kerapatan ρ₁ = 0,75ρ dan jari-jari R₁ = 1,25 R, maka percepatan gravitasinya menjadi

g’ = 4πG(0,75ρ)(1,25R)/3 = (15/16)[4πGρR/3]

g’ = 15g/16

Soal 5
Percepatan gravitasi pada permukaan bumi adalah g. Pada permukaan planet yang massanya sama dengan bumi tetapi massa jenisnya dua kali Bumi percepatan gravitasi akan menjadi . . . .
A. 2^-2/3g
B. 2^-1/3g
C. g
D. 1^1/3g
E. 2^2/3g

Jawab: E
Percepatan gravitasi sebuah planet dinyatakan oleh

g_p = GM_p/r_P²

Percepatan gravitasi Bumi dinyatakan oleh

g = GM_B/r_B²

massa jenis planet dua kali massa jenis Bumi, maka

M_P/(4πr_P³/3) = 2M_B/(4πr_B³/3)

½ = (R_P/R_B)³

R_P/R_B = (½)^1/3

Perbandingan percepatan gravitasi keduanya diberikan oleh

g_P/g = (M_P/M_B)(r_B/r_P)²

atau
g_P/g = (2^1/3)²

g_P = 2^2/3g