Soal 1
Balok bermassa 2M diletakkan diatas bidang miring yang koefisien gesekan statisnya µs, dan dihubungkan dengan benda lain bermassa M melalui katrol licin dengan memakai tali yang massanya diabaikan seperti gambar diatas. Kemiringan bidang dapat diatur. Jika sudut φ diperbesar, maka pada saat mencapai sudut φm balok dalam keadaan hampir meluncur turun. Pada keadaan ini berlaku hubungan . . . .
A. 1 + 2µs cos φm = 2sinφm
B. 1 + µs cos φm = 2sinφm
C. 1 + 2µs cos φm = sinφm
D. 1 + 2µs cos φm = 2cosφm
E. 1 + µs cos φm = 2cosφm
Jawab: A
Gaya-gaya yang bekerja pada balok ditunjukkan pada gambar di bawah ini,
Hukum II Newton memberikan
a = ΣF/m
a = [2Mg sinφ – T + T – f – Mg]/3M
atau
a = [2Mg sinφ – f – Mg]/3M
dengan f = µN = 2µsMg cosφ, maka
a = [2Mg sinφ – 2µsMg cosφ – Mg]/3M
Pada saat mencapai sudut φm balok dalam keadaan hampir meluncur turun, artinya
a ≥ 0 = [2Mg sinφm – 2µs Mg cosφm – Mg]/3M
2Mg sinφm – 2µs Mg cosφm – Mg = 0
2µscosφm + 1 = 2 sinφm
Soal 2
Balok A dan beban gantung B dihubungkan dengan tali dan dipasang pada landasan licin seperti pada gambar. Landasan terpasang tepat pada lantai mendatar. Perbandingan tinggi dan panjang alas adalah 3 : 4. Tali dianggap cukup kuat, tidak elastis, dan massanya diabaikan.
Gesekan katrol juga diabaikan. Jika massa A adalah 0,5 kg, massa B adalah 1,1 kg, dan percepatan gravitasi dianggap 10 m/s2, percepatan balok A dan tegangan tali berturut-turut adalah . . . .
A. 3,4 m/s2 dan 5 N
B. 5 m/s2 dan 3,4 N
C. 5 m/s2 dan 5 N
D. 5 m/s2 dan 5,5 N
E. 5,5 m/s2 dan 5 N
Jawab: D
Gaya-gaya yang bekerja pada sistem balok ditunjukkan di bawah ini,
Hukum II Newton memberikan
a = ΣF/m = [mBg – T + T – mAg sinφ]/(mA + mB)
a = [mBg – mAg sinφ]/(mA + mB)
= [(1,1 kg)– (0,5 kg)(0,6)](10 m/s2)/(0,5 kg + 1,1 kg)
a = 5 m/s2
untuk balok B, berlaku
ΣFB = mBa
mBg – T = mBa
(1,1 kg)(10 m/s2) – T = (1,1 kg)(5 m/s2)
T = 5,5 N
Soal 3
Perhatikan gambar!
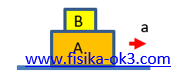
Balok B berada di atas balok A. Balok A bermassa 15 kg, sedangkan balok B bermassa 10 kg. Kedua balok bergerak dengan percepatan konstan a = 2 m/s2 ke kanan dan koefisien gesekan statis antara kedua balok adalah µs = 0,6 . Gaya gesekan statis yang bekerja pada kedua balok tersebut adalah . . . .
A. 10 N
B. 20 N
C. 30 N
D. 40 N
E. 60 N
Answer: C
Gaya gesek statis pasti muncul antara kedua balok A dan B, karena kedua balok bergerak bersama-sama (balok B diam terhadap A).
Dengan hukum II Newton pada balok B, kita peroleh
∑FB = mBa
fBA = mBa = (15 kg)(2 m/s2) = 30 N
Soal 4
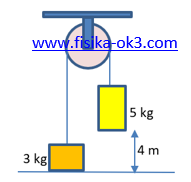
Tinggi maksimum yang dapat dicapai benda B diukur dari lantai adalah . . . . (g = 10 m/s2)
A. 4 m
B. 5 m
C. 6 m
D. 7 m
E. 8 m
Jawab: B
Gaya-gaya yang bekerja pada sistem balok ditunjukkan pada gambar di bawah ini,
Ketika dilepas, sistem (balok m1 dan m2) akan mengalami percepatan sebesar
a = ∑F/m
a = (50 N – T + T – 30 N)/(3 kg + 5 kg) = 2,5 m/s2
Balok m2 naik dengan percepatan 2,5 m/s2 sampai sejauh 4 m (karena balok m1 sudah menumbuk lantai), hal ini tidak berarti bahwa m2 juga berhenti pada ketinggian 4 m, karena kecepatan m2 belum tentu nol saat itu.
Oleh karena itu kita cari dahulu kecepatan m2 pada ketinggian 4 m (m2 dipercepat ke atas dengan percepatan 2,5 m/s2) dengan menggunakan,
v2 = v02 + 2aΔy
v2 = 0 + 2(2,5 m/s2)(4 m)
v = 2√5 m/s
Saat kecepatan m2 mencapai 2√2 m/s, balok m2 akan mengalami perlambatan sebesar –10 m/s2 dalam sampai ketinggian maksimum (v = 0) dalam waktu,
v = v0 + ayt
0 = 2√5 m/s – (10 m/s2)t
t = 0,2√5 s
maka tinggi maksimum yang dicapai m2 adalah
y = y0 + v0yt + ½ ayt2
ym = 4 m + (2√5 m/s)(0,2√5 s) + ½ (–10 m/s2)(0,2√5 s)2
ym = 4 m + 2 m – 1 m = 5 m
Balok bermassa 2M diletakkan diatas bidang miring yang koefisien gesekan statisnya µs, dan dihubungkan dengan benda lain bermassa M melalui katrol licin dengan memakai tali yang massanya diabaikan seperti gambar diatas. Kemiringan bidang dapat diatur. Jika sudut φ diperbesar, maka pada saat mencapai sudut φm balok dalam keadaan hampir meluncur turun. Pada keadaan ini berlaku hubungan . . . .
A. 1 + 2µs cos φm = 2sinφm
B. 1 + µs cos φm = 2sinφm
C. 1 + 2µs cos φm = sinφm
D. 1 + 2µs cos φm = 2cosφm
E. 1 + µs cos φm = 2cosφm
Gaya-gaya yang bekerja pada balok ditunjukkan pada gambar di bawah ini,
Hukum II Newton memberikan
a = ΣF/m
a = [2Mg sinφ – T + T – f – Mg]/3M
atau
a = [2Mg sinφ – f – Mg]/3M
dengan f = µN = 2µsMg cosφ, maka
a = [2Mg sinφ – 2µsMg cosφ – Mg]/3M
Pada saat mencapai sudut φm balok dalam keadaan hampir meluncur turun, artinya
a ≥ 0 = [2Mg sinφm – 2µs Mg cosφm – Mg]/3M
2Mg sinφm – 2µs Mg cosφm – Mg = 0
2µscosφm + 1 = 2 sinφm
Soal 2
Balok A dan beban gantung B dihubungkan dengan tali dan dipasang pada landasan licin seperti pada gambar. Landasan terpasang tepat pada lantai mendatar. Perbandingan tinggi dan panjang alas adalah 3 : 4. Tali dianggap cukup kuat, tidak elastis, dan massanya diabaikan.
Gesekan katrol juga diabaikan. Jika massa A adalah 0,5 kg, massa B adalah 1,1 kg, dan percepatan gravitasi dianggap 10 m/s2, percepatan balok A dan tegangan tali berturut-turut adalah . . . .
A. 3,4 m/s2 dan 5 N
B. 5 m/s2 dan 3,4 N
C. 5 m/s2 dan 5 N
D. 5 m/s2 dan 5,5 N
E. 5,5 m/s2 dan 5 N
Jawab: D
Gaya-gaya yang bekerja pada sistem balok ditunjukkan di bawah ini,
Hukum II Newton memberikan
a = ΣF/m = [mBg – T + T – mAg sinφ]/(mA + mB)
a = [mBg – mAg sinφ]/(mA + mB)
= [(1,1 kg)– (0,5 kg)(0,6)](10 m/s2)/(0,5 kg + 1,1 kg)
a = 5 m/s2
untuk balok B, berlaku
ΣFB = mBa
mBg – T = mBa
(1,1 kg)(10 m/s2) – T = (1,1 kg)(5 m/s2)
T = 5,5 N
Soal 3
Perhatikan gambar!
Balok B berada di atas balok A. Balok A bermassa 15 kg, sedangkan balok B bermassa 10 kg. Kedua balok bergerak dengan percepatan konstan a = 2 m/s2 ke kanan dan koefisien gesekan statis antara kedua balok adalah µs = 0,6 . Gaya gesekan statis yang bekerja pada kedua balok tersebut adalah . . . .
A. 10 N
B. 20 N
C. 30 N
D. 40 N
E. 60 N
Answer: C
Gaya gesek statis pasti muncul antara kedua balok A dan B, karena kedua balok bergerak bersama-sama (balok B diam terhadap A).
Dengan hukum II Newton pada balok B, kita peroleh
∑FB = mBa
fBA = mBa = (15 kg)(2 m/s2) = 30 N
Soal 4
Tinggi maksimum yang dapat dicapai benda B diukur dari lantai adalah . . . . (g = 10 m/s2)
A. 4 m
B. 5 m
C. 6 m
D. 7 m
E. 8 m
Jawab: B
Gaya-gaya yang bekerja pada sistem balok ditunjukkan pada gambar di bawah ini,
Ketika dilepas, sistem (balok m1 dan m2) akan mengalami percepatan sebesar
a = ∑F/m
a = (50 N – T + T – 30 N)/(3 kg + 5 kg) = 2,5 m/s2
Balok m2 naik dengan percepatan 2,5 m/s2 sampai sejauh 4 m (karena balok m1 sudah menumbuk lantai), hal ini tidak berarti bahwa m2 juga berhenti pada ketinggian 4 m, karena kecepatan m2 belum tentu nol saat itu.
Oleh karena itu kita cari dahulu kecepatan m2 pada ketinggian 4 m (m2 dipercepat ke atas dengan percepatan 2,5 m/s2) dengan menggunakan,
v2 = v02 + 2aΔy
v2 = 0 + 2(2,5 m/s2)(4 m)
v = 2√5 m/s
Saat kecepatan m2 mencapai 2√2 m/s, balok m2 akan mengalami perlambatan sebesar –10 m/s2 dalam sampai ketinggian maksimum (v = 0) dalam waktu,
v = v0 + ayt
0 = 2√5 m/s – (10 m/s2)t
t = 0,2√5 s
maka tinggi maksimum yang dicapai m2 adalah
y = y0 + v0yt + ½ ayt2
ym = 4 m + (2√5 m/s)(0,2√5 s) + ½ (–10 m/s2)(0,2√5 s)2
ym = 4 m + 2 m – 1 m = 5 m







Post a Comment for "Soal Hukum Newton dan Pembahasannya 3"
Sobat Fisika! Berikan Komentar di kolom komentar dengan bahasa yang sopan dan sesuai isi konten...Terimasih untuk kunjunganmu di blog ini, semoga bermanfaat!