Soal 1
Sebuah peti kecil dengan massa 6 kg yg bertumpu pada dua rodanya sedang melaju dengan kelajuan 4 m/s diatas lantai es horizontal. Anggap tidak ada gesekan pada lantai es.
(a). Berapa besar gaya henti P yg membentuk sudut α (sin α = 5/13) yang mampu menghentikan peti setelah menempuh jarak 3,2 m?
(b). Berapa besar gaya normal yg di kerjakan lantai es pada tiap roda peti? (gaya normal pada tiap roda = setengah gaya normal total)
Jawab:
(a) peti tersebut bergerak arah horisontal dengan kecepatan awal 4 m/s, maka gaya henti yang bekerja pada arah horisontal adalah P cosα yang memberikan perlambatan pada peti sebesar
a = –P cosθ/m
a = –P (12/13)/6 kg = –2P/13
karena peti berhenti (v = 0), maka
v2 = v02 + 2aΔx
0 = (4 m/s)2 + (–2P/13)(3,2 m)
P = 208/6,4 = 32,5 N
(b) Peti tidak bergerak pada arah sumbu y, maka
∑Fy = 0
2N – P sinα – mg = 0
N = ½ (P sinα + mg)
N = ½ [32,5 N(5/13) + (6 kg)(10 m/s2)] = 36,25 N
Soal 2
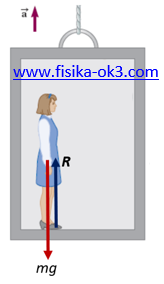
Seorang gadis dengan massa 60kg sedang berada di dalam sebuah elevator pusat pertokotan. Tentukan besar gaya yang dikerjakan kedua telapak kaki gadis itu pada elevator ketika : (g = 9,8 m/s2)
a. Elevator diam
b. Elevator bergerak keatas dengan kecepatan tetap
c. Elevator bergerak kebawah dengan kecepatan tetap
d. Elevator bergerak keatas dengan percepatan 4m/s2
e. Elevator bergerak keatas dengan perlambatan 2m/s2
f. Elevator bergerak kebawah dengan percepatan 4m/s2
g. Kabel penahan elevator putus dan elevator jatuh bebas
Jawab:
(a) Jika elevator diam, maka berlaku
∑Fy = 0
R – mg = 0
R = mg = (60 kg)(10 m/s2) = 60 N
(b) dan (c) elevator bergerak ke atas dengan kecepatan tetap, artinya ∑Fy = 0, maka R = mg = 60 N.
(d) Elevator bergerak ke atas dengan percepatan 4m/s2, maka
∑Fy = ma
R – mg = ma
R = m(g + a) = (60 kg)(10 m/s2 + 4 m/s2) = 840 N
(e) Elevator bergerak ke atas dengan perlambatan 2m/s2, maka
∑Fy = ma
R – mg = –ma
R = m(g – a) = (60 kg)(10 m/s2 – 4 m/s2) = 360 N
(f) Elevator bergerak ke bawah dengan percepatan 4m/s2, maka
∑Fy = ma
–R + mg = ma
R = m(g – a) = (60 kg)(10 m/s2 – 4 m/s2) = 360 N
(g)Kabel penahan elevator putus dan elevator jatuh bebas, maka gadis tersebut jatuh bebas, maka R = 0.
Soal 3
Karyawan bagian desain sebuah pabrik mendesain sebuah elevator yang dapat menampung 20 orang dengan massa rata-rata 65 kg. Elevator itu sendiri bermassa 500 kg. Hasil uji kekuatan tarik menunjukkan bahwa kabel pendukung elevator mampu mentoleransi gaya maksimum 29.600 N. Berapa percepatan terbesar yang dapat dihasilkan motor elevator tanpa memutuskan kabel?
(g = 9,8 m/s2)
Jawab:
Resultan gaya maksimum yang bekerja pada tali ∑F = 29600 N. Percepatan elevator yang diperboleh adalah sebesar
a = ∑F/m = 29600 N/(20 x 65 kg + 500 kg)
a = 16,4 m/s2
Soal 5
Sistem pada gambar berikut sedang bergerak ke atas dengan percepatan a. Hitung tegangan tali T1, T2, T3 ketika sistem itu sedang bergerak (nyatakan dalam m1, m2, m3, a dan g).
Jawab
Gaya-gaya yang bekerja pada sistem benda ditunjukkan pada gambar di bawah ini,
Dengan menerapkan hukum II Newton pada sistem benda di atas, kita peroleh
a = ∑F/m = (T1 – m1g – T2 + T2 – m2g – T3 + T3 – m3g)/(m1 + m2 + m3)
a = (T1 – m1g – m2g – m3g)/(m1 + m2 + m3)
(m1 + m2 + m3)a = (T1 – m1g – m2g – m3g)
T1 = (m1 + m2 + m3)a + (m1 + m2 + m3)g
T1 = (m1 + m2 + m3)(g + a)
Pada benda m1 berlaku
a = ∑F1/m1 = (T1 – T2)/m1
m1a = (m1 + m2 + m3)a + (m1 + m2 + m3)g – T2
T2 = (m2 + m3)a + (m1 + m2 + m3)g
Pada benda m2 berlaku
a = ∑F2/m2 = (T2 – T3)/m2
m2a = (m2 + m3)a + (m1 + m2 + m3)g – T3
T2 = m3a + (m1 + m2 + m3)g
Sebuah peti kecil dengan massa 6 kg yg bertumpu pada dua rodanya sedang melaju dengan kelajuan 4 m/s diatas lantai es horizontal. Anggap tidak ada gesekan pada lantai es.
(a). Berapa besar gaya henti P yg membentuk sudut α (sin α = 5/13) yang mampu menghentikan peti setelah menempuh jarak 3,2 m?
(b). Berapa besar gaya normal yg di kerjakan lantai es pada tiap roda peti? (gaya normal pada tiap roda = setengah gaya normal total)
Jawab:
(a) peti tersebut bergerak arah horisontal dengan kecepatan awal 4 m/s, maka gaya henti yang bekerja pada arah horisontal adalah P cosα yang memberikan perlambatan pada peti sebesar
a = –P cosθ/m
a = –P (12/13)/6 kg = –2P/13
karena peti berhenti (v = 0), maka
v2 = v02 + 2aΔx
0 = (4 m/s)2 + (–2P/13)(3,2 m)
P = 208/6,4 = 32,5 N
(b) Peti tidak bergerak pada arah sumbu y, maka
∑Fy = 0
2N – P sinα – mg = 0
N = ½ (P sinα + mg)
N = ½ [32,5 N(5/13) + (6 kg)(10 m/s2)] = 36,25 N
Soal 2
Seorang gadis dengan massa 60kg sedang berada di dalam sebuah elevator pusat pertokotan. Tentukan besar gaya yang dikerjakan kedua telapak kaki gadis itu pada elevator ketika : (g = 9,8 m/s2)
a. Elevator diam
b. Elevator bergerak keatas dengan kecepatan tetap
c. Elevator bergerak kebawah dengan kecepatan tetap
d. Elevator bergerak keatas dengan percepatan 4m/s2
e. Elevator bergerak keatas dengan perlambatan 2m/s2
f. Elevator bergerak kebawah dengan percepatan 4m/s2
g. Kabel penahan elevator putus dan elevator jatuh bebas
Jawab:
(a) Jika elevator diam, maka berlaku
∑Fy = 0
R – mg = 0
R = mg = (60 kg)(10 m/s2) = 60 N
(b) dan (c) elevator bergerak ke atas dengan kecepatan tetap, artinya ∑Fy = 0, maka R = mg = 60 N.
(d) Elevator bergerak ke atas dengan percepatan 4m/s2, maka
∑Fy = ma
R – mg = ma
R = m(g + a) = (60 kg)(10 m/s2 + 4 m/s2) = 840 N
(e) Elevator bergerak ke atas dengan perlambatan 2m/s2, maka
∑Fy = ma
R – mg = –ma
R = m(g – a) = (60 kg)(10 m/s2 – 4 m/s2) = 360 N
(f) Elevator bergerak ke bawah dengan percepatan 4m/s2, maka
∑Fy = ma
–R + mg = ma
R = m(g – a) = (60 kg)(10 m/s2 – 4 m/s2) = 360 N
(g)Kabel penahan elevator putus dan elevator jatuh bebas, maka gadis tersebut jatuh bebas, maka R = 0.
Soal 3
Karyawan bagian desain sebuah pabrik mendesain sebuah elevator yang dapat menampung 20 orang dengan massa rata-rata 65 kg. Elevator itu sendiri bermassa 500 kg. Hasil uji kekuatan tarik menunjukkan bahwa kabel pendukung elevator mampu mentoleransi gaya maksimum 29.600 N. Berapa percepatan terbesar yang dapat dihasilkan motor elevator tanpa memutuskan kabel?
(g = 9,8 m/s2)
Jawab:
Resultan gaya maksimum yang bekerja pada tali ∑F = 29600 N. Percepatan elevator yang diperboleh adalah sebesar
a = ∑F/m = 29600 N/(20 x 65 kg + 500 kg)
a = 16,4 m/s2
Soal 5
Sistem pada gambar berikut sedang bergerak ke atas dengan percepatan a. Hitung tegangan tali T1, T2, T3 ketika sistem itu sedang bergerak (nyatakan dalam m1, m2, m3, a dan g).
Jawab
Gaya-gaya yang bekerja pada sistem benda ditunjukkan pada gambar di bawah ini,
Dengan menerapkan hukum II Newton pada sistem benda di atas, kita peroleh
a = ∑F/m = (T1 – m1g – T2 + T2 – m2g – T3 + T3 – m3g)/(m1 + m2 + m3)
a = (T1 – m1g – m2g – m3g)/(m1 + m2 + m3)
(m1 + m2 + m3)a = (T1 – m1g – m2g – m3g)
T1 = (m1 + m2 + m3)a + (m1 + m2 + m3)g
T1 = (m1 + m2 + m3)(g + a)
Pada benda m1 berlaku
a = ∑F1/m1 = (T1 – T2)/m1
m1a = (m1 + m2 + m3)a + (m1 + m2 + m3)g – T2
T2 = (m2 + m3)a + (m1 + m2 + m3)g
Pada benda m2 berlaku
a = ∑F2/m2 = (T2 – T3)/m2
m2a = (m2 + m3)a + (m1 + m2 + m3)g – T3
T2 = m3a + (m1 + m2 + m3)g




Post a Comment for "Soal Hukum Newton dan Pembahasannya 5"
Sobat Fisika! Berikan Komentar di kolom komentar dengan bahasa yang sopan dan sesuai isi konten...Terimasih untuk kunjunganmu di blog ini, semoga bermanfaat!