Soal 1
Dua balok dengan masing-masing 3 kg dan 5 kg dihubungkan dengan tali. Kedua balok bergerak menuruni bidang miring dengan sudut kemiringan θ = 370. Koefisien gesekan kinetis untuk balok 3 kg adalah 0,4, sedangkan untuk balok 5 kg adalah 0,3. Tentukan percepatan masing-masing balok dan tegangan dalam tali (sin 370 = 0,6).
Jawab:
Gaya-gaya yang bekerja pada setiap balok ditunjukkan pada gambar di bawah ini,
Untuk setiap balok kita ambil +x menurun (yang mengarah ke kiri bawah pada diagram ini) dan +y searah gaya normal.
Sepenuhnya menggambarkan dinamika sistem selama balok miliki percepatan dan T > 0 yang sama.
Balok 1:
∑Fy1 = 0
N1 – 50 cos370 = 0
N1 = 50 cos370 = 40 N
Maka gaya gesek yang bekerja pada balok 1 adalah
f1 = µ1N1 = 0,3(40 N) = 12N, sehingga pada
∑Fx1 = m1a
50 sin370 – T – f1 = 5a
30 – T – 12 = 5a
18 – T = 5a (*)
Balok 2:
∑Fy2 = 0
N2 – 30 cos370 = 0
N2 = 30 cos370 = 24 N
Maka gaya gesek yang bekerja pada balok 2 adalah
f2 = µ2N2 = 0,4(24 N) = 9,6 N, sehingga pada
∑Fx1 = m1a
30 sin370 + T – f2 = 3a
18 + T – 9,6 = 3a
8,4 + T = 3a (**)
Jumlahkan (*) dan (**), kita peroleh
26,4 = 8a
a = 3,3 m/s2
Tegangan tali diberikan oleh
8,4 + T = 3a
T = 3(3,3 m/s2) – 8,4 = 1,5 N
Soal 2
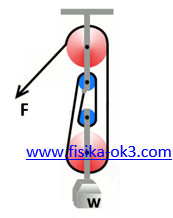
Sebuah sistem katrol adalah suatu mesin sederhana yang digunakan untuk mengangkat benda berat, berapakah besar gaya F yang harus di kerjakan untuk menahan sebuah beban seberat w tetap di tempatnya. Abaikan massa tali dan katrol.
Jawab:
Sistem katrol ini menerapkan gaya 4F, sehingga memiliki keuntungan mekanis ≈ 4.
Besarnya F adalah 4F = w, atau
F = ¼ w
Soal 3
Diagram berikut menunjukkan sebuah balok bermassa 2 kg bergantung pada seutas tali yang dihubungkan ke sebuah kereta-keretaan. (Sistem dipertahankan diam oleh kait H). Anggap gesekan sistem dan massa katrol dapat diabaikan, serta permukaan meja datar.
Tentukan: (a) Gaya yang dikerjakan pada gerobak oleh kait H, dan (b) jika kereta-keretaan dilepaskan dari kait H, tentukan percepatan benda dan gaya tegangan tali.
Jawab:
Gaya-gaya yang bekerja pada sistem ditunjukkan pada gambar di bawah ini,
(a) R adalah gaya yang dikerjakan kait pada gelobak. Jika sistem dipertahankan diam oleh kait H, maka berlaku
20 N – T + T – R = 0
R = 20 N
(b) Jika kereta dilepaskan dari kait H, maka R = 0, dengan menggunakan hukum II Newton percepatan balok dan kereta diberikan oleh
a = ∑F/m
a = (20 N – T + T)/(5 kg) = 4 m/s2
dan tegangan tali kita peroleh dari
T = mka = 3kg(4 m/s2) = 12 N
Dua balok dengan masing-masing 3 kg dan 5 kg dihubungkan dengan tali. Kedua balok bergerak menuruni bidang miring dengan sudut kemiringan θ = 370. Koefisien gesekan kinetis untuk balok 3 kg adalah 0,4, sedangkan untuk balok 5 kg adalah 0,3. Tentukan percepatan masing-masing balok dan tegangan dalam tali (sin 370 = 0,6).
Jawab:
Gaya-gaya yang bekerja pada setiap balok ditunjukkan pada gambar di bawah ini,
Untuk setiap balok kita ambil +x menurun (yang mengarah ke kiri bawah pada diagram ini) dan +y searah gaya normal.
Sepenuhnya menggambarkan dinamika sistem selama balok miliki percepatan dan T > 0 yang sama.
Balok 1:
∑Fy1 = 0
N1 – 50 cos370 = 0
N1 = 50 cos370 = 40 N
Maka gaya gesek yang bekerja pada balok 1 adalah
f1 = µ1N1 = 0,3(40 N) = 12N, sehingga pada
∑Fx1 = m1a
50 sin370 – T – f1 = 5a
30 – T – 12 = 5a
18 – T = 5a (*)
Balok 2:
∑Fy2 = 0
N2 – 30 cos370 = 0
N2 = 30 cos370 = 24 N
Maka gaya gesek yang bekerja pada balok 2 adalah
f2 = µ2N2 = 0,4(24 N) = 9,6 N, sehingga pada
∑Fx1 = m1a
30 sin370 + T – f2 = 3a
18 + T – 9,6 = 3a
8,4 + T = 3a (**)
Jumlahkan (*) dan (**), kita peroleh
26,4 = 8a
a = 3,3 m/s2
Tegangan tali diberikan oleh
8,4 + T = 3a
T = 3(3,3 m/s2) – 8,4 = 1,5 N
Soal 2
Sebuah sistem katrol adalah suatu mesin sederhana yang digunakan untuk mengangkat benda berat, berapakah besar gaya F yang harus di kerjakan untuk menahan sebuah beban seberat w tetap di tempatnya. Abaikan massa tali dan katrol.
Jawab:
Sistem katrol ini menerapkan gaya 4F, sehingga memiliki keuntungan mekanis ≈ 4.
Besarnya F adalah 4F = w, atau
F = ¼ w
Soal 3
Diagram berikut menunjukkan sebuah balok bermassa 2 kg bergantung pada seutas tali yang dihubungkan ke sebuah kereta-keretaan. (Sistem dipertahankan diam oleh kait H). Anggap gesekan sistem dan massa katrol dapat diabaikan, serta permukaan meja datar.
Tentukan: (a) Gaya yang dikerjakan pada gerobak oleh kait H, dan (b) jika kereta-keretaan dilepaskan dari kait H, tentukan percepatan benda dan gaya tegangan tali.
Jawab:
Gaya-gaya yang bekerja pada sistem ditunjukkan pada gambar di bawah ini,
(a) R adalah gaya yang dikerjakan kait pada gelobak. Jika sistem dipertahankan diam oleh kait H, maka berlaku
20 N – T + T – R = 0
R = 20 N
(b) Jika kereta dilepaskan dari kait H, maka R = 0, dengan menggunakan hukum II Newton percepatan balok dan kereta diberikan oleh
a = ∑F/m
a = (20 N – T + T)/(5 kg) = 4 m/s2
dan tegangan tali kita peroleh dari
T = mka = 3kg(4 m/s2) = 12 N





Post a Comment for "Soal Hukum Newton dan Pembahasannya 7"
Sobat Fisika! Berikan Komentar di kolom komentar dengan bahasa yang sopan dan sesuai isi konten...Terimasih untuk kunjunganmu di blog ini, semoga bermanfaat!