Soal 1
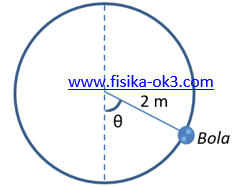
Sebuah bola bermassa 0,60 kg diikat pada ujung seutas kawat dan diayun dalam suatu lingkaran vertikal. Panjang kawat adalah 2 m. Pada saat tali membentuk sudut θ, laju bola 6 m/s dan tegangan kawat adalah 12,8 N. Tentukan nilai θ!
Jawab:
Gaya-gaya yang bekerja pada bola ditunjukkan seperti gambar di bawah ini,
∑F = ma
T – mg cosθ = mv2/r
12,8 N – 0,6 kg(10 m/s2) cosθ = (0,6 kg)(6 m/s)2/(2 m)
12,8 N – 6 cosθ = 10,8 N
θ = cos-1(1/3) = 70,50
Soal 2
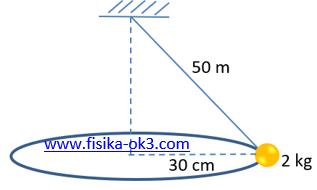
Sebuah bandul bermassa 2 kg digantung pada seutas tali dengan panjang 50 cm. Benda itu bergerak dalam suatu lingkaran horizontal dengan radius 30 cm dengan kelajuan tetap (lihat gambar). Hitung:
(a) tegangan tali, (b) gaya sentripetal yang bekerja pada bandul, dan (c) periode bandul dalam orbit lingkaran.
Jawab:
(a) Pada sumbu y berlaku
∑Fy = 0
T cosθ – mg = 0
T = mg/cosθ
T = (2kg)(10 m/s2)/0,8 = 25 N
(b) gaya sentripetal yang bekerja pada bandul adalah
∑Fx = Fs = T sinθ
Fs = 25N(0,6) = 15 N
(c). periode bandul dalam orbit lingkaran.
Fs = mω2r
dengan ω = 2π/T, maka
Fs = 4π2mr/T2
15 N = 4π2(2 kg)(0,3 m)/T2
T2 = 1,6
T = 1,26 s
Soal 3
Tarzan berencana untuk menyebrangi sebuah jurang dengan cara mengayun dalam sebuah busur yang dibentuk oleh akar gantung pepohonan. Jika tangannya hanya mampu mengerjakan gaya sebesar 1.200 N pada tali, berapakah laju maksimum Tarzan yang dapat ditoleransi pada titik terendah ayunannya? (massa Tarzan 90 kg, panjang akar gantung 4,9 m, dan g = 10 m/s²).
Jawab:
Gaya-gaya yang bekerja pada Tarzan ditunjukkan pada gambar di bawah ini.
Dengan hukum II Newton kita peroleh
∑F = ma
T – w = mv2/r
1200 N – 900 N = (90 kg)v2/(4,9 m)
v2 = 30(4,9)/9
v = 4,04 m/s
Soal 4
Titi melajukan mobilnya dengan kelajuan tetap 9 m/s ketika melalui suatu jalan berbukit. Jalan berbukit dapat dianggap berbentuk busur lingkaran dengan jari-jari 11 m. (a) Jika berat Titi adalah 550 N, berapakah berat semunya ketika mobil berada di puncak jalan berbukit? Dan (b) Jika Titi ingin mengalami keadaan tanpa bobot ketika berada di puncak jalan berbukit, dengan laju berapakah ia harus melajukan mobilnya?
Jawab:
(a) berat semu Titi adalah N, maka dengan hukum II Newton pada puncak bukit, kita peroleh
∑F = ma
mg – N = mv2/r
550 N – N = (55 kg)(9 m/s)2/(11 m)
N = 550 N – 405 N = 145 N
(b) keadaan tanpa bobot artinya berat semu Titi sama dengan nol, N = 0 maka
mg – N = mv2/r
mg = mv2/r
v = (gr)1/2
v = [(10 m/s2)(11 m)]1/2 = 10,5 m/s
Soal 5
Seorang insinyur diminta untuk merancang jalan ke luar tol dengan radius 50 m. Persyaratannya adalah walaupun kondisi jalan sangat licin, mobil dapat membelok pada batas kelajuan 72 km/jam tanpa slip. Berapakah sudut kemiringan belokan yang harus dibuat insinyur itu?
Jawab:
sudut kemiringan belokan yang harus dibuat insinyur itu adalah
tan θ = v2/gr
tan θ = (20 m/s)2/[(10 m/s2)(50 m)]
θ = tan-1(4/5) = 38,60
Sebuah bola bermassa 0,60 kg diikat pada ujung seutas kawat dan diayun dalam suatu lingkaran vertikal. Panjang kawat adalah 2 m. Pada saat tali membentuk sudut θ, laju bola 6 m/s dan tegangan kawat adalah 12,8 N. Tentukan nilai θ!
Jawab:
Gaya-gaya yang bekerja pada bola ditunjukkan seperti gambar di bawah ini,
∑F = ma
T – mg cosθ = mv2/r
12,8 N – 0,6 kg(10 m/s2) cosθ = (0,6 kg)(6 m/s)2/(2 m)
12,8 N – 6 cosθ = 10,8 N
θ = cos-1(1/3) = 70,50
Soal 2
Sebuah bandul bermassa 2 kg digantung pada seutas tali dengan panjang 50 cm. Benda itu bergerak dalam suatu lingkaran horizontal dengan radius 30 cm dengan kelajuan tetap (lihat gambar). Hitung:
(a) tegangan tali, (b) gaya sentripetal yang bekerja pada bandul, dan (c) periode bandul dalam orbit lingkaran.
Jawab:
(a) Pada sumbu y berlaku
∑Fy = 0
T cosθ – mg = 0
T = mg/cosθ
T = (2kg)(10 m/s2)/0,8 = 25 N
(b) gaya sentripetal yang bekerja pada bandul adalah
∑Fx = Fs = T sinθ
Fs = 25N(0,6) = 15 N
(c). periode bandul dalam orbit lingkaran.
Fs = mω2r
dengan ω = 2π/T, maka
Fs = 4π2mr/T2
15 N = 4π2(2 kg)(0,3 m)/T2
T2 = 1,6
T = 1,26 s
Soal 3
Tarzan berencana untuk menyebrangi sebuah jurang dengan cara mengayun dalam sebuah busur yang dibentuk oleh akar gantung pepohonan. Jika tangannya hanya mampu mengerjakan gaya sebesar 1.200 N pada tali, berapakah laju maksimum Tarzan yang dapat ditoleransi pada titik terendah ayunannya? (massa Tarzan 90 kg, panjang akar gantung 4,9 m, dan g = 10 m/s²).
Jawab:
Gaya-gaya yang bekerja pada Tarzan ditunjukkan pada gambar di bawah ini.
Dengan hukum II Newton kita peroleh
∑F = ma
T – w = mv2/r
1200 N – 900 N = (90 kg)v2/(4,9 m)
v2 = 30(4,9)/9
v = 4,04 m/s
Soal 4
Titi melajukan mobilnya dengan kelajuan tetap 9 m/s ketika melalui suatu jalan berbukit. Jalan berbukit dapat dianggap berbentuk busur lingkaran dengan jari-jari 11 m. (a) Jika berat Titi adalah 550 N, berapakah berat semunya ketika mobil berada di puncak jalan berbukit? Dan (b) Jika Titi ingin mengalami keadaan tanpa bobot ketika berada di puncak jalan berbukit, dengan laju berapakah ia harus melajukan mobilnya?
Jawab:
(a) berat semu Titi adalah N, maka dengan hukum II Newton pada puncak bukit, kita peroleh
∑F = ma
mg – N = mv2/r
550 N – N = (55 kg)(9 m/s)2/(11 m)
N = 550 N – 405 N = 145 N
(b) keadaan tanpa bobot artinya berat semu Titi sama dengan nol, N = 0 maka
mg – N = mv2/r
mg = mv2/r
v = (gr)1/2
v = [(10 m/s2)(11 m)]1/2 = 10,5 m/s
Soal 5
Seorang insinyur diminta untuk merancang jalan ke luar tol dengan radius 50 m. Persyaratannya adalah walaupun kondisi jalan sangat licin, mobil dapat membelok pada batas kelajuan 72 km/jam tanpa slip. Berapakah sudut kemiringan belokan yang harus dibuat insinyur itu?
Jawab:
sudut kemiringan belokan yang harus dibuat insinyur itu adalah
tan θ = v2/gr
tan θ = (20 m/s)2/[(10 m/s2)(50 m)]
θ = tan-1(4/5) = 38,60





Post a Comment for "Soal Hukum Newton, Gaya Sentripetal dan Pembahasannya 3"
Sobat Fisika! Berikan Komentar di kolom komentar dengan bahasa yang sopan dan sesuai isi konten...Terimasih untuk kunjunganmu di blog ini, semoga bermanfaat!