Soal kesetimbangan benda tegar dan penyelesaiannya 3

Soal 1:
Untuk Sistem di bawah ini, jika berat batang pejal 40 N dan berat beban 60 N. Tentukan besar T₁, T₂ dan T₃!

jawab:
Sistem dalam keadaan setimbang maka gaya-gaya yang bekerja pada titik A dan batang seperti gambar di bawah ini

Gaya-gaya yang bekerja pada titik A untuk sumbu y membertikan,
T₂ sin 45⁰ = 60 N
T₂ = 60/sin 45⁰ = 60√2 N
Gaya-gaya yang bekerja pada titik A untuk sumbu x membertikan,
T₁ = T₂ cos 45⁰ = (60√2 N) cos 45⁰ = 60 N
Batang dalam keadaan setimbang dengan mengambil poros di titik B, maka
Στ_B = 0
– T₂L + (T₃ sin 30⁰) x L + (40N) x (½ L cos 45⁰) = 0
– (60√2 N)L + T₃ (½L) – (20N) L (½√2) = 0

T₃ = 140√2 N 

Soal 2:

Sistem pada gambar dalam keadaan setimbang statis. Tentukan besar T₁, T₂ dan berat batang!

Jawab:
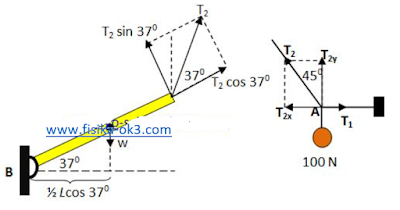
Diagram gaya yang bekerja pada sistem seperti ditunjukan pada gambar

Gaya-gaya yang bekerja pada titik A untuk sumbu y memberikan
T_2y = 100 N = T₂ cos 45⁰
T₂ = 100 N/cos 45⁰ = 100√2 N
Gaya-gaya yang bekerja pada titik A untuk sumbu x memberikan
T₁ = T_2x = T₂ sin 45⁰
T₂ = (100√2 N) sin 45⁰ = 100 N
Gaya-gaya yang bekerja pada batang memberikan torsi pada titik B, maka
Στ_B = 0
(T₂ sin 37⁰)L – w(½ Lcos 37⁰) = 0
(100 N)(3/5) = w (1/2)(4/5)
w = 150 N

Soal 3:

Sebuah balok batang seragam diengsel pada tanah dan berdiri tegak seperti pada sistem gambar di bawah ini. Tentukan besar T₁, T₂ dan gaya-gaya yang bekerja pada engsel!

Jawab:
Gaya-gaya bebas yang bekerja pada benda ditunjukkan pada gambar di bawah ini,

Dari sistem benda 100 N, kita peroleh
T₁ – 100 N = 0
T₁ = 100 N
Dengan mengambil poros pada titik A, kita rumuskan
Στ_A = 0
T_2x (L/2) + (– T₁L) = 0
T₂ (cos 37⁰) = 2(100 N)
T₂ = 250 N
Jumlah gaya-gaya pada sumbu x sama dengan nol
ΣF_x = 0
T₁ + F_x – T_2x = 0
F_x = T_2x – T₁ =  T₂ (cos 37⁰) – 100 N
F_x = (250 N)(cos 37⁰) – 100 N
F_x = 100 N
Jumlah gaya-gaya pada sumbu x sama dengan nol
ΣF_y = 0
F_y – T_2y = 0
F_y = T₂ sin 37⁰ = (250 N) sin 37⁰
F_y = 150 N