Soal Tumbukan dan Pembahasannya

 Soal#5

Sebuah peluru 20 g bergerak dengan kecepatan 50 m/s bersarang dalam balok 7 kg yang diam di atas lantai. Hitunglah (a). kecepatan balok setelah tumbukan (b). gaya gesekan antara balok dan meja jika balok berpindah sejauh 1,5 m hingga berhenti.

 

Jawab:
(a) Dengan menggunakan hukum kekekalan momentum antara peluru dan balok, dan v_p = 50 m/s, m_p = 20 g, m_b = 7 kg, maka

m_pv_p + m_bv_b = (m_p + m_b)v
(20 x 10^-3 kg)(50 m/s) + 0 =  (20 x 10^-3 kg + 7 kg)v
v = 0,14 m/s

(b) besar perlambatan akibat gaya gesek adalah ½
Wnk = ∆EK
-fs = - ½ mv²
f(1,5 m) = ½ (0,02 + 7)(1/(7,002))² → f = 0,045 N
  
Soal#6
Sebuah peluru 15 g ditembakan secara horisontal mengarah ke sebuah balok 3 kg yang digantung dengan tali panjang seperti pada Gambar. Peluru bersarang dalam balok dan balok berayun sampai ke ketinggian 10 cm di atas titik semula. Berapa kecepatan peluru?
   

Jawab:
Hukum kekekalan momentum memberikan,
m_pv_p + m_bv_b = (m_p + m_b)v
(15 x 10^-3 kg)(v_p) + 0 =  (15 x 10^-3 kg + 3 kg)v
v_p = 201v (*)
setelah tumbukan peluru bersarang dalam balok dan bersama balok naik setinggi 10 cm, berlaku hukum kekekalan energy,

½ (m_p + m_b)v² = (m_p + m_b)gh
v = √(2gh) = √(2 x 10 x 0,1) = √2 m/s, maka dari (*) diperoleh
v_p = 201√2 m/s


Soal #7
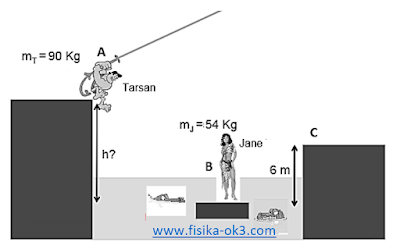
Pada suatu ketika Jane (54 kg) terjebak dalam oleh kerumunan buaya yang ingin memaksanya dalam suatu danau yang tenang di tengah hutan. Ketika itu Tarsan (90 kg) yang berada di sebuah tebing setinggi h diukur dari perahu Jane berayun dengan menggunakan tali dan menyelamatkan Jane dan tiba di tebing lainnya setinggi 6 m. Jika tarsan bergerak dari keadaan diam dan bersama Jane diam di tebing lainnya. Tentukan h!

 

Jawab:

Gerakan Tarsan dari A ke B, berlaku hukum kekekalan energi mekanik, maka
EP_A + EK_A = EP_B + EK_B

m_Tgh + 0 = 0 + ½ m_Tv_T²  (v_T = kecepatan tarsan)
v_T = √(2gh) = √(20h)

ketika di B berlaku hukum kekekalan momentum, maka

m_Tv_T + m_Jv_J = (m_T + m_J)v_TJ
(90 kg)(√(20h m/s) + 0 = (90 kg + 54 kg)v_TJ

Untuk mencari v_TJ, kita menggunakan lagi hukum kekekalan energi mekanik untuk gerakan dari B ke C, maka

EP_C + EK_C = EP_B + EK_B
m_TJgy + 0 = 0 + ½ m_TJv_TJ²  (v_T = kecepatan tarsan)

v_TJ = √(2gy) = √(20 x 6) = √120 m/s

sehingga dari persamaan sebelumnya kita dapatkan

(90 kg)(√(20h m/s) + 0 = (90 kg + 54 kg)(√120 m/s)
90² x 20h = 144² x 120
h = 15,36 m

Soal#8
Sebuah bola baja dijatuhkan dari dari ketinggian 0,5 m di atas lantai . Setelah tumbukan bola naik hingga ketinggian 0,4 m. Tentukan koefisien restitusi e untuk situasi ini.

 

Jawab

Awalnya bola jatuh bebas dengan kecepatan awal nol. Bola akan tiba di tanah dengan kecepatan,

Tanda negatif karena arah ke bawah. 


Setelah tumbukan bola bergerak meninggalkan lantai dengan kecepatan


Benda kedua adalah lantai, sebelum dan sesudah tumbukkan tetap dalam keadaan diam maka


Oleh 

untuk kasus ini, 

Share :